Question

A block of mass $3kg$ is placed on the floor of coefficient of static friction $0.4$. A force of $3.5N$ is applied on the block. Calculate the force of friction and discuss the motion of the body.
$A)3.5N$, moves
$B)3.4N$, remains at rest
$C)11.76N$, moves
$D)11.76N$, remains at rest

Answer 1

Frictional force is a self-adjusting force, if the external force applied on a body is less than the force of friction. Maximum static friction is called as limiting friction, which is nothing but the frictional force acting on a body, when the body just begins to move over a surface. Limiting friction is mathematically equal to the product of weight of the body and the coefficient of static friction.
Formula used:
${{F}_{\max }}={{\mu }_{s}}mg$

Complete answer:
It is given that a block of mass $3kg$ is placed on a floor of coefficient of static friction $0.4$. An external force of $3.5N$ is applied on the block. We are required to find the force of friction acting on the block. We are also told to discuss the motion of the block.
When a body of particular mass is placed on a floor, a frictional force acts on the body. This frictional force is called static friction. Coefficient of static friction is defined as the ratio of static friction acting on a body to the normal force acting on that body. The maximum value of static friction is defined as the frictional force acting on a body, when the body just begins to move. This maximum value of static friction is termed as limiting friction. Limiting friction always acts opposite to the motion of the body.
Limiting friction of a body is mathematically equal to the product of weight of the body and the coefficient of static friction. It is given by
${{F}_{\max }}={{\mu }_{s}}mg$
where
${{F}_{\max }}$ is the limiting friction or the maximum static friction.
${{\mu }_{s}}$ is the coefficient of static friction.
$m$ is the mass of the body.
$g$ is the acceleration due to gravity.
Let this be equation 1.

Let us calculate the limiting friction for the block, provided in the question.
We know that the mass of the block is $3kg$ and the coefficient of static friction is $0.4$. Taking the value of $g$ as $10m{{s}^{-2}}$, we have
${{F}_{\max }}={{\mu }_{s}}mg=0.4\times 2kg\times 10m{{s}^{-2}}=8N$
where
${{F}_{\max }}$ is the limiting friction of the block
Let this be equation 2.

Now, it is said that an external force of $3.5N$ is applied on the block. Let this external force be represented as ${{F}_{ext}}$.Clearly,
${{F}_{ext}}=3.5N$
Let this be equation 3.
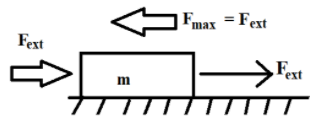
Limiting friction is a self-adjusting force for a body at rest. If the external force applied on a body is less than the limiting friction of the body, the limiting friction adjusts itself to be equal to the external force applied on the body.
In our case,
${{F}_{ext}}(3.5N)<{{F}_{\max }}(8N)$
Therefore, the liming friction of the block adjusts itself to be equal to the external force acting on the body. Limiting friction of the block is now given by
${{F}_{\max }}={{F}_{ext}}=3.5N$
Hence, the block will experience a force of $3.5N$ and this force will cause the block to move in the direction of the external force applied.

The correct option to be marked is $A$.

Note:
Students might wonder why the block doesn’t remain at rest even when the maximum static friction is greater than the external force. All we need to understand is that frictional forces are self-adjusting forces for bodies at rest. In such cases, the maximum frictional force acting on the body at rest reduces to the external force and makes the body move from rest. It is also important to remember that frictional force always opposes the direction of motion of a body.