Question

A block of mass $3{\text{kg}}$ starts from rest and slides down an advanced path in the shape of a quarter circle of radius $2{\text{m}}$ and reaches the bottom of the path with a speed of $4{\text{m}}{{\text{s}}^{ - 1}}$ . If $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ , find the amount of work done against friction.

Answer 1

As the block moves along the advanced path, its potential energy will get converted into kinetic energy. But due to friction, work has to be done against the frictional forces for the block to reach the bottom of the path. So the total energy of the block will not be conserved.
Formula used:
The potential energy of a body at a height $h$ is given by, $U = mgh$ where $m$ is the mass of the body and $g$ is the acceleration due to gravity.
The kinetic energy of a body is given by, $K = \dfrac{1}{2}m{v^2}$ where $v$ is the velocity of the body and $m$ is the mass of the body.

Complete answer:
Step 1: Sketch the advanced path along which the block moves and list its parameters.
The advanced path takes the shape of the first quadrant of a circle.

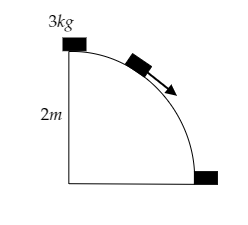
The mass of the block is given to be $m = 3{\text{kg}}$ .
The radius of the circle is given to be $r = 2{\text{m}}$ .
The velocity at the bottom of the path is given to be $v = 4{\text{m}}{{\text{s}}^{ - 1}}$ .
Also, the acceleration due to gravity is given to be $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ .
Step 2: Express the potential energy of the block at top of the path.
The potential energy of the block at the top of the path of height $h$ can be expressed as $U = mgh$ .
Here the block is placed at a height equal to the radius of the circle i.e., $h = r$ and so we have $U = mgr$ --------- (1)
Substituting for $m = 3{\text{kg}}$ , $r = 2{\text{m}}$ and $g = 10{\text{m}}{{\text{s}}^{ - 2}}$ in equation (1) we get, $U = 3 \times 10 \times 2 = 60{\text{J}}$
Thus the potential energy of the block is $U = 60{\text{J}}$ .
Step 3: Express the kinetic energy of the block at the bottom of the path.
The kinetic energy of the block at the bottom of the path can be expressed as
$K = \dfrac{1}{2}m{v^2}$ -------- (2)
Substituting for $m = 3{\text{kg}}$ and $v = 4{\text{m}}{{\text{s}}^{ - 1}}$ in equation (2) we get, $K = \dfrac{1}{2} \times 3 \times {4^2} = 24{\text{J}}$
Thus the kinetic energy of the block at the bottom of the path is $K = 24{\text{J}}$.
Step 4: Express the work done against friction based on the conservation of energy.
If the total energy of the block was conserved then the loss in its potential energy will be the gain in its kinetic energy i.e., $\Delta U = \Delta K$ .
But here the total energy is not conserved and so the potential energy of the block will be the sum of its kinetic energy and work done against friction.
Thus we have the work done against friction as ${W_f} = U - K$ --------- (3)
Substituting for $U = 60{\text{J}}$ and $K = 24{\text{J}}$ in equation (3) we get, ${W_f} = 60 - 24 = 36{\text{J}}$
Thus the work done against friction will be ${W_f} = 36{\text{J}}$ .

Note:
Here at the top of the path, the block only possesses potential energy and at the bottom of the path the block only possesses kinetic energy. A part of the potential energy of the block gets converted into kinetic energy of the block and the other part is used to do work against the frictional forces so that the block can move along the path. This work will then be dissipated as heat to the surroundings.