Question

A block of mass 2kg is placed on the floor. The coefficient of static friction is ${\mu _s} = 0.4$. If a force of 2.8 N is applied on the block parallel to the floor, the force of friction between the block and the floor (taking $g = 10m/{\sec ^2}$) is-
a) 2.8N
b) 8N
c) 2N
d) Zero

Answer 1

Hint- We will put all the values given in the question into the formula of force of friction to find the required answer. We will also take help of a figure in order to understand the solution better as done below-

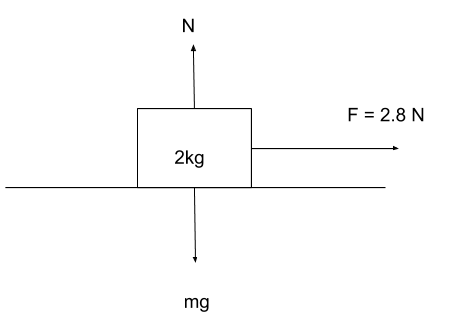
Formula used: $f = \mu N$.

Complete step-by-step answer:

The mass of the block as given in the question is 2kg.
The coefficient of static friction is 0.4.
Force applied on the block is ${F_{net}} = 2.8N$.
The force of friction between the block and the floor =?
Since we know that the formula of friction is- $f = \mu N$. Where f is friction, $\mu$ is the coefficient and N stands for normal force.
Now, we know that the value of N with the help of the figure i.e.-
$\Rightarrow N = mg$
Putting this value of N in the above formula for friction, we get-
$\Rightarrow f = \mu mg$
We know that the value of coefficient is 0.4, the value of m is the mass of the block i.e. 2kg and g is the gravitational force which is 10m/${\sec ^2}$as per given in the question. Putting all the values in $f = \mu mg$, we get-
$\Rightarrow f = \mu mg \\\ \\\ \Rightarrow f = 0.4 \times 2 \times 10 \\\ \\\ \Rightarrow f = 8N \\\$
As we can see that the above value of friction i.e. 8N is more than the net force-
$\Rightarrow f > {F_{net}}$
Since, the applied force is less than the force of friction, the friction adjusts its value and the new value becomes 2.8N so that block remains in equilibrium.
Thus, $f = 2.8N$.
Hence, option a) is the correct option.

Note: Remember that whenever the applied force is less than the force of friction, the force of friction will always adjust itself because it cannot be more than the value of applied force. Do not leave the answer at the calculated value of friction which is more than the net force.