Question
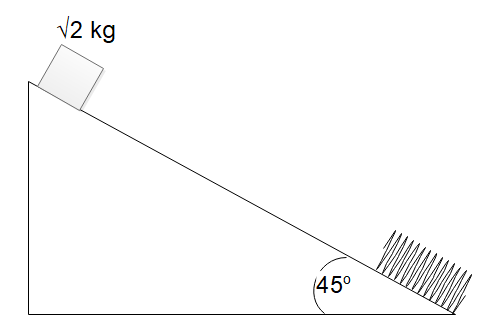
Question: A block of mass 2kg is released from the top of an inclined smooth surface as shown in the figure. ...
A block of mass 2kg is released from the top of an inclined smooth surface as shown in the figure. If the spring constant of spring is 100 N/m and the block comes to rest after compressing the spring by 1 m, then the distance travelled by block before it comes to rest is
A) 1 m
B) 1.25m
C) 2.5m
D) 5 m
Solution
Hint : In this solution, we will use the law of conservation of energy to determine the compression of the spring. At the top of the ramp, the block will only have potential energy due to its height and when it is compressing the spring, it will transfer all its energy into the potential energy of the spring.
Formula used: In this solution, we will use the following formula:
Potential energy due to height: U=mgh where m is the mass of the block, g is the gravitational acceleration, and h is its height above the ground.
Potential energy of spring: E=21kx2 where k is the spring constant and x is the compression of the spring
Complete step by step answer
We’ve been given that a block of mass 2kg is released from the top of an inclined smooth surface and it slips down the drop eventually coming in contact with the spring and compressing it.
When the block is at the top of the ramp, it will have gravitational potential energy associated with its height from the ground according to the relation
⇒U=mgh
When it slips down and interacts with e spring and compresses it, all its energy will be converted into potential energy of the spring due which we can calculate as:
⇒E=21kx2
Since the total energy of the system will remain constant, the potential energy of the block at the top of the ramp will be converted totally to the potential energy of the spring, so we can write
⇒mgh=21kx2
Let s be the distance the block travels then the height of the block above the ground will be h=ssin45∘ , so
⇒mgssin45∘=21kx2
Substituting the appropriate values,
⇒2(10)s(21)=21(100)(1)2
So, we can solve for s , we get
⇒s=5m which corresponds to option (D).
Note
Because of the law of conservation of energy, we only need to focus on the initial and the final position of the block and not its trajectory in between, since there will not be any energy losses associated with friction. In the middle of its trajectory, the block will have potential and kinetic energy, but when it compresses the spring, it will come to rest and convert it’s kinetic and potential energy into the potential energy of the spring.
