Question

A block of mass 1Kg is free to move along the $X$ axis. It is at rest and from time $t = 0$ onwards it is subjected to a time- dependent force $F\left( t \right)$ varies with $t$ as shown in figure. The kinetic energy of the block at $t = 4\,s$ is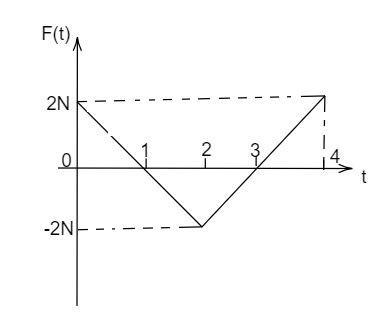
(A) $1\,J$
(B) $2\,J$
(C) $3\,J$
(D) $0\,J$
(E) $4\,J$

Answer 1

Hint :Analyze the graph given, and separate the graph into different regions. The sum of the area of the graph provides the momentum of the block. From the answer, find the velocity of the block. Substitute the velocity in the kinetic energy formula to find the kinetic energy of the block.
Formula used:
(1) The area of the triangle is given by

$A = \dfrac{1}{2}bh$

Where $A$ is the area of the considered triangle, $b$ is the base of the triangle and $h$ is the height or the altitude of the triangle.

(2) The kinetic energy is given by

$KE = \dfrac{1}{2}m{v^2}$
Where $KE$ is the kinetic energy of the block, $m$ is the mass of the block and $v$ is the velocity of the block.

Completes step by step solution:
It is given that the
Mass of the block, $m = 1\,Kg$

The block moves by the external force applied on it, and its movement covers the area of three triangles. Hence the total area of the graph provides the movement of the block. The sum of the area of the three triangles provides the total area of the triangles.

$M = A$

$M = {A_1} + {A_2} + {A_3}$

Let us find the base and the height value of the three triangles in the graph by using the coordinates. The base and the height value of the first and the third triangle is $1$ and $2$ respectively. The base and the height value of the second triangle is $2$ and $2$ respectively. Substituting these values in the formula of the area,

$M = \dfrac{1}{2} \times 1 \times 2 - \dfrac{1}{2} \times 2 \times 2 + \dfrac{1}{2} \times 1 \times 2$

By performing basic arithmetic operations in it, we get

$M = 0$

Hence the momentum is obtained as zero. We know that the momentum is the product of the mass and the velocity.

$M = mv = 0$
$v = 0$

Hence the velocity is also obtained as zero. Using the kinetic energy formula,

$KE = \dfrac{1}{2}m{v^2}$

Substituting the value of the velocity as zero, we get

$KE = 0\,J$

Thus the option (D) is correct.

Note: The second triangle is located below the horizontal $X$ axis, hence the area of this triangle from the others to find the total area formed by the motion of the block. The kinetic energy of the block as zero represents that the block stops at the time $4\,s$ .