Question

A block of mass $1kg$ is at rest on a horizontal table. The coefficient of static friction between the block and the table is $0.50$ if $g = 10m/{s^2}$ then the magnitude of force acting upwards at an angle of $60^\circ$ from horizontal that will just start the block moving is.
A. $5N$
B. $5.36N$
C. $74.6N$
D. $10N$

Answer 1

We can solve this question by applying a simple law of vector. We have to equate all horizontal forces and all vertical forces which are acting on the block. The coefficient of static friction is given in question with the help of this can calculate the friction force and the force acting opposite to it must be equal to this so the block can just start to move.

Complete step by step answer:
As shown in figure we mark all the forces which can act on the block in this condition

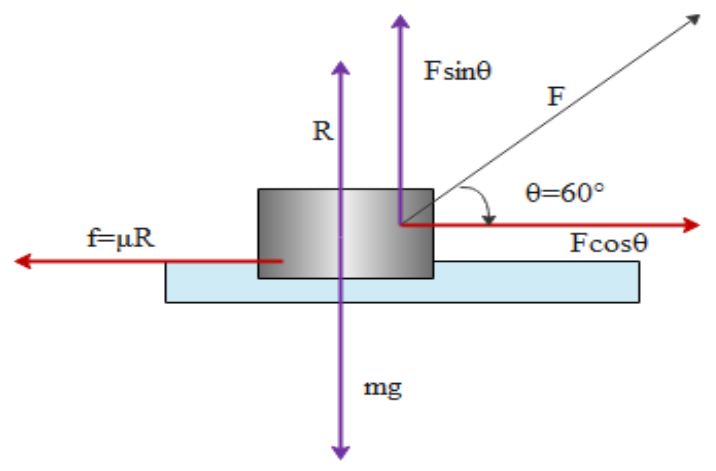
Force acting on the block
Weight of block downward direction
Normal reaction $R$ upward direction
Vertical component of applied force $F\sin \theta$
And horizontal forces
Horizontal component of force $F\cos \theta$
Friction force between block and table $f = \mu R$
Values are given in question
$m = 1kg$ $g = 10m/{s^2}$ $\mu = 0.5 = \dfrac{1}{2}$ $\theta = 60^\circ$
Now equate vertical forces
$\Rightarrow mg = R + F\sin \theta$
$\Rightarrow R = mg - F\sin \theta$
Put given value
$\Rightarrow R = 10 - F\sin 60^\circ$
$\Rightarrow R = 10 - \dfrac{{\sqrt 3 }}{2}F$
Friction force given as $f = \mu R$
$f = 0.5\left( {10 - \dfrac{{\sqrt 3 }}{2}F} \right)$........... (1)
Now equate all the horizontal forces
$f = F\cos \theta$
$\Rightarrow f = F\cos 60^\circ$
$\Rightarrow f = \dfrac{F}{2}$
Put value from equation (1)
$\dfrac{F}{2} = 0.5\left( {10 - \dfrac{{\sqrt 3 }}{2}F} \right)$
$F = 2 \times 0.5\left( {10 - \dfrac{{\sqrt 3 }}{2}F} \right)$
Solving this
$\Rightarrow F = 10 - \dfrac{{\sqrt 3 }}{2}F$
Rearranging this
$\Rightarrow F + \dfrac{{\sqrt 3 }}{2}F = 10$
$\Rightarrow 2F + \sqrt 3 F = 20$
$\Rightarrow F\left( {2 + \sqrt 3 } \right) = 20$
So the value of applied force
$\Rightarrow F = \dfrac{{20}}{{\left( {2 + \sqrt 3 } \right)}}$
$\therefore F = 5.36N$

So, the correct answer is “Option B”.

Note:
Sometime student makes a very common mistake while solving this question, calculating friction force friction force given by $f = \mu R$ and some student learn it as $f = \mu mg$ which is not always correct it is correct only when applied force is in horizontal direction so be careful to calculate friction force.