Question

A block of mass $1kg$ and a pan of equal mass are connected by a string going over a smooth pulley. Initially the system is at rest when a particle of mass falls on the pan and strikes it. If the particle strikes the pan with the speed $v=6m/s$ then the speed with which the system moves just after the collision.

& \text{A}\text{. }3m/s \\\ & \text{B}\text{. }4m/s \\\ & \text{C}\text{. }2.5m/s \\\ & \text{D}\text{. }2m/s \\\ \end{aligned}$$

Answer 1

First we have to draw a diagram to understand the system and from the diagram itself we can understand the forces acting in the system and by balancing the forces we can find the speed of the system just after collision. Here we will be using impulse acting on the block, pan and the particle.

Formula used:
Impulse (I) = Force (F) $\times$ time (t)

Complete answer:
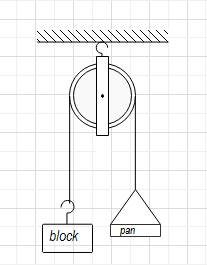
It is given that a block and a pan of equal masses connected by a string going over a smooth pulley which can be shown as follow

Now a particle of the same mass is approaching towards the pan with velocity v when the system is at rest.

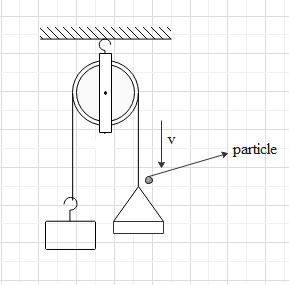
The moment the particle strikes the pan, there will be an impulse generated. (Impulse is the force acting on a system for a specific duration of time and it is given as product of force and the time)
Now the moment a particle strikes on the pan there will be a normal force acting in the upward direction of the pan and the downward tension of the string. The particle will be having a normal upward direction and change in velocity. Let the change in velocity of the system be V after the collision. And there will be an upward tension of string which will be experienced by block. The net downward gravitational force will be cancelled out. The system and the force can be shown as

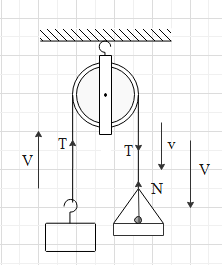
We have to find V, for which we can calculate the impulse for the block, pan and the particle which can be given as
Impulse on the particle ${{I}_{1}}=\int{Ndt=m(v-V)}$
Impulse on the pan ${{I}_{2}}=\int{(N-T)dt=mV}$
Impulse on the block ${{I}_{3}}=\int{Tdt=mV}$

As the collision takes place and changes are sudden and short therefore integral are used. From the above equations we can write

& \Rightarrow {{I}_{2}}={{I}_{1}}-{{I}_{3}} \\\ & \Rightarrow mV=m(v-V)-mV \\\ & \Rightarrow mV=mv-mV-mV \\\ & \Rightarrow 3mV=mv \\\ & \Rightarrow V=\dfrac{v}{3} \\\ \end{aligned}$$ Substituting value of $$v=6m/s$$ $$V=\dfrac{6}{3}=2m/s$$ Hence the system will move with $$2m/s$$ just after the collision. The correct option is D. **So, the correct answer is “Option D”.** **Note:** The tension for the block and the pan will be the same as they are connected with the same string. As the tension is created due to the moment in the string. The downward gravitational force experienced by the block and the pan will be nullified and therefore we have not considered it. The mass of the block, pan and the particle is the same.