Question

A block of mass $15kg$ is resting on a rough inclined plane as shown in Fig. The block is tied by a horizontal string which has a tension of $50N$. The coefficient of friction between the surfaces of contact is
$(A)\dfrac{1}{2}$
$(B)\dfrac{2}{3}$
$(C)\dfrac{3}{4}$
$(D)\dfrac{1}{4}$

Answer 1

In this question, the frictional force is exerted in the direction opposite to the motion of the object which is caused by the gravitational force. For the block to not move in any of the directions, whether forward or backward, the forces which are not acting on the block need to be balanced to get the equilibrium. The formula of friction is,
$f = \mu N$, where $F$ is the frictional force, $\mu$ is the coefficient of friction and $N$ is the normal reaction.

Complete step by step answer:
On resolving the forces acting on the block in the horizontal and the vertical direction, we get the following figure:
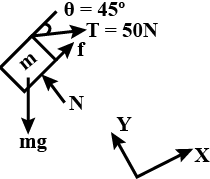ha)
The force acting on the horizontal direction,
$\sum {{F_X} = 0}$ given
$mg\sin \theta = f - T\cos \theta$
Where, $f$ is the force of friction
On taking $f$ on one side and all the other terms on the other side, we get,
$f = mg\sin \theta - T\cos \theta$
We also know that $f = \mu N$, so the above equation can be written as,
$\mu N = mg\sin \theta - T\cos \theta ......(1)$
Similarly, in the vertical direction,
$\sum {{F_Y} = 0}$ given
$N = mg\cos \theta + T\sin \theta ......(2)$
On dividing equation (1) by equation (2), we get,
$\dfrac{{\mu N}}{N} = \dfrac{{mg\sin \theta - T\cos \theta }}{{mg\cos \theta + T\sin \theta }}$
$\mu = \dfrac{{mg\sin \theta - T\cos \theta }}{{mg\cos \theta + T\sin \theta }}$
On putting the required values, we get,
$\mu = \dfrac{{15 \times 10 \times \sin {{45}^ \circ } - 50\cos {{45}^ \circ }}}{{15 \times 10 \times \cos {{45}^ \circ } + 50\sin {{45}^ \circ }}}$
$\mu = \dfrac{{150\sin {{45}^ \circ } - 50\cos {{45}^ \circ }}}{{150\cos {{45}^ \circ } + 50\sin {{45}^ \circ }}}$
On putting the value of the trigonometric functions, we get,
$\mu = \dfrac{{150\left( {\dfrac{1}{{\sqrt 2 }}} \right) - 50\left( {\dfrac{1}{{\sqrt 2 }}} \right)}}{{150\left( {\dfrac{1}{{\sqrt 2 }}} \right) + 50\left( {\dfrac{1}{{\sqrt 2 }}} \right)}}$
On further solving the above equation, we get,
$\mu = 0.5$
$\mu = \dfrac{1}{2}$
So, the correct answer is $(A)\dfrac{1}{2}$.

Note: It is important to note that, when inclined planes are taken into consideration, the force does not act in linear directions as it usually acts. We know that the force is a vector, so the direction of actual application of the force on the object determines the effects of it. We have to break the forces into the inclined components to derive the net force equations and solve them.