Question

A block of mass 10 kg is placed on a rough horizontal surface and is acted upon by a variable force F horizontally. The coefficient of friction between block and surface is $\mu =0.5$ The force F, starting from a value of zero is increased linearly to 100 N in 4 s and then abruptly decreased to 40 N which is then continued for 3 sec. And then the force is removed.
A. The maximum velocity reached by the block is 5m/s
B. The time of motion of block is 5.4sec.
C. The maximum velocity reached by the block is at time 22 sec. after the start of
motion of the block
D. friction on block will be 25N at time 1s after the force begins to act

Answer 1

We have to calculate the normal force, then we will calculate the limiting friction, after calculating the limiting friction we have to draw the graph for the problem given in the question now from the graph we will have to calculate the impulse and then find the velocity at t = 4s. Now calculate the time of motion and force at t= 1 sec and then compare all the options with the values we found.
Formula Used:
$f=\mu \times N$
$impulse={{P}_{F}}-{{P}_{i}}$

Complete answer:

Now, the normal force will be, N = 10g
$N=10\times 10N$
$N=100N$
Here according to the question we can see a block of mass 10 kg and on which there is a variable force acting horizontally.
Now, we know that there is a friction of $\mu =0.5$ acting between the block and the floor, and we also know the mass of the body, So we can calculate the limiting friction by the formula,
$f=\mu \times N$ ,
On putting the values in the above equation we get,
$f=0.5\times 100$
$f=50N$
Now we can say that at time(t) = 2 sec the force acting on the block is 50N but no motion is there as the friction is balancing the force applied so net force will be zero.
Now, at time t = 4 sec, there is a the force gets increased to 100N,

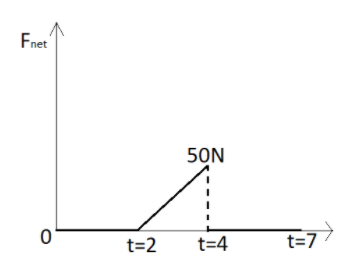
Now at t = 2 sec velocity ${{v}_{1}}=0$ so there is no net motion.
Now when t = 4 sec velocity ${{v}_{2}}=v$
Now we will see the phenomenon for impulse, which is actually the change in momentum
$impulse={{P}_{F}}-{{P}_{i}}$…….Eq.1
Now, calculating momentum from t = 2 sec to t = 4 sec.
$impulse(j)=\dfrac{1}{2}\times 50\times (4-2)$
So, $impulse(j)=50$…….Eq.2
Now,
${{P}_{F}}$ will be ${{P}_{F}}=m{{v}_{2}}=10\times v=10v$…… Eq.3
And ${{P}_{i}}=m{{v}_{1}}=0$as ${{v}_{1}}=0$……..Eq.4
Now, placing all the values of Eq.2, Eq.3, Eq.4 into Eq.1 we get,
$\Rightarrow 50=10v$
Which on solving gives us,
$v=5m/s$
Now, this is the maximum velocity at t=4sec.
Now, at t = 4+3 = 7 sec.
After placing values in equation 1, we get,
$\Rightarrow -50(t-7)=10\times 2$
Which gives t= 7.4 seconds.
Now, therefore the time of motion will be, t = 7.4 – 2 = 5.4 sec
Now, when t=1sec then F = 25.

So, from all the explanations given above we see that all options A, B, C, D all are correct.

Note:
The solution to this question is very vast and each and every step needs precision. There are many formulas working all at a same time so students may get confused so proper remembrance of formulas are required. In this formula $impulse={{P}_{F}}-{{P}_{i}}$, ${{P}_{F}}$ is the final momentum and ${{P}_{i}}$ is the initial momentum.