Question

A block of mass 10 kg is placed on a rough horizontal surface whose coefficient of friction is 0.5. If a horizontal force of 100 N is applied on it, then acceleration of the block will be:
[Take $g=10m{{s}^{-2}}$ ]
A. $10m{{s}^{-2}}$
B. $5m{{s}^{-2}}$
C. $15m{{s}^{-2}}$
D. $0.5m{{s}^{-2}}$

Answer 1

First we need to construct the free body diagram (a diagram showing the magnitude and direction of all the forces acting on the body) of the block. Using the equation to find frictional force and equating it with force acting on the body (by Newton’s second law) we get the acceleration.

Formula used:
Friction,
$f=\mu N$
Force,
$F=ma$

Complete step-by-step solution:
We have a block placed horizontally on a rough surface.
It is said that a force of 100N is applied on the block.
Let’s’ be the mass of the block, we are given that,
m = 10Kg
The coefficient of friction between the surface and the block is also given,
$\mu =0.5$ were ‘$\mu$’ is the coefficient of friction
Let us consider the free body diagram of the block as shown below,

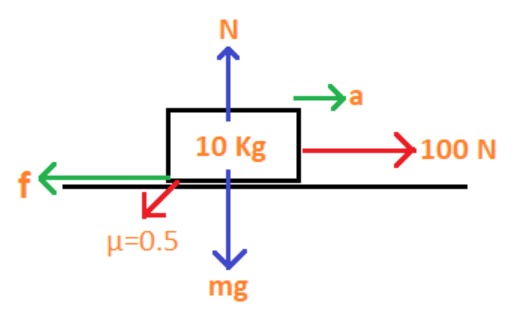
From the figure, we can see that the force is acting horizontally towards the right.
We know that frictional force is opposite to the direction of force; therefore here friction is acting horizontally towards the left.
The other two forces acting on the body are the weight of the body which acts vertically downwards and normal force that acts vertically upwards.
Since these two forces are in opposite direction, we can say that
$N=mg$, were ‘N’ is normal force and ‘mg’ is the weight of the body.
We know, the frictional force is given by the equation,
$f=\mu N$
Substituting ‘mg’ instead of ‘N’, we get
$f=\mu mg$
We know the values of ‘$\mu$’, ‘m’, and ‘g’.
Therefore,
$\begin{aligned} & f=0.5\times 10\times 10 \\\ &\Rightarrow f=50N \\\ \end{aligned}$
Therefore, we have a force of 100N acting horizontally towards right and frictional force acting horizontally towards left on the block.
Hence the net force acting on the block will be,
$\begin{aligned} & F=100-50 \\\ &\Rightarrow F=50N \\\ \end{aligned}$
Also, from Newton’s second law of motion we know that,
$F=ma$
Therefore, we can equate the two equations of force, we get
$ma=50$
By solving this we get the acceleration of the block ‘a’ as,
$\begin{aligned} & a=\dfrac{50}{m} \\\ &\Rightarrow a=\dfrac{50}{10} \\\ \end{aligned}$
$\Rightarrow a=5m/{{s}^{2}}$
Therefore the acceleration of the block is $5m{{s}^{-2}}$
Hence the correct answer is option B.

Note: Here we got the frictional force as, $f=\mu N=50N$.
This friction experienced here is the limiting friction.
Limiting friction is the maximum friction formed between two static surfaces in contact with each other.
Therefore, limiting friction ${{f}_{L}}=50N$.
We know that if the force applied is less than the limiting friction, then the body will not move.
However here the applied force is 100N, which is greater than the frictional force (50N); therefore the body moves forward with an acceleration of $5m/{{s}^{2}}$.