Question
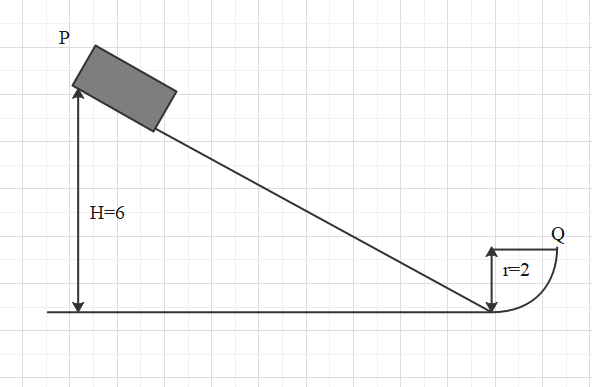
Question: A block of mass 1 kg is released from P on a frictionless track which ends in quarter circular track...
A block of mass 1 kg is released from P on a frictionless track which ends in quarter circular track of radius 2 m at the bottom. What is the magnitude of radial acceleration and total acceleration of the block when it arrives at Q?
Solution
Since the block is released from a certain height, so calculate the loss of height. We get the displacement of the object. Then by using the formula: v2=u2+2gs , find the final velocity of the block. Now, we know that the radial acceleration is given by: aR=rv2 and tangential acceleration is given by: aT=g . So, total acceleration is: a=(aR)2+(aT)2 .
Formula used:
v2=u2+2gs, where v is final velocity, u is initial velocity, g is the acceleration due to gravity and s is the distance covered.
aR=rv2, where aRis the radial acceleration, v is the velocity and r is the radius.
aT=g, where aT is the tangential acceleration and g is the acceleration due to gravity
a=(aR)2+(aT)2, where a is the total acceleration, aRis the radial acceleration and aT is the tangential acceleration.
Complete step by step answer:
We have:
h1=6m h2=2m u=0m/s m=1kg
So, the displacement of the block is:
⇒s=(6−2) ⇒s=4m
Now, by using the Newton’s law of motion: v2=u2+2gs
We get:
⇒v2=0+(2×9.81×4) ⇒v2=78.48m2s−2
As we know that:
The radial acceleration is given by: aR=rv2
So, we have:
⇒aR=278.48 ⇒aR=39.2ms−2
So, total acceleration is:
⇒a=(aR)2+(aT)2 ⇒a=(39.2)2+(9.81)2 ∴a=40.4ms−2
Note:
We have been given a block that is at rest and then it accelerates as it is released from the point P. The block is released from a certain height therefore its potential energy is converted into kinetic energy. So, by conserving the total energy, we can write:
ΔPE=ΔKE ⟹−mg(h2−h1)=21m(v2−u2) ⟹(6−2)=21v2 ∴78.48=v2
