Question

A block of mass $0.1kg$ is held against a wall by applying a horizontal force of $5N$ on the block. If the coefficient of friction between the block and the wall is $0.5$ , Find the magnitude of the frictional force acting on the block is.

Answer 1

Hint : Use the condition for static equilibrium of the block to find the frictional force acting on it. Condition for equilibrium is given by, ${F_{net}} = 0$ . For a body in rest frictional force acting is $f = \mu N$ where $\mu$ is the coefficient of static friction and $N$ is the normal force by the surface the body is placed.

Complete Step By Step Answer:
We know if a body is in equilibrium that means either moving with constant velocity or is at rest then, net force acting on it is zero. ${F_{net}} = 0$ .
Here, we have a block held on a wall. So, the net force acting on the block must be zero since the block is static.
Now, the block is being given a force of normally. Hence, the normal force given by the surface of the wall will also be $5N$ .
Now, we can see, vertically on the block there are two forces acting on the block. First one is the gravitational pull of the earth and the other is the frictional force.
Here we have the gravitational pull, $mg = 0.1 \times 9.8 = 0.98N$ . The maximum frictional force that can act on the body is,
${f_{\max }} = {\mu _s}N$ .
Putting the values of $\mu = 0.5$ and $N = 5$ we get , ${f_{\max }} = 0.5 \times 5 = 2.5N$ .

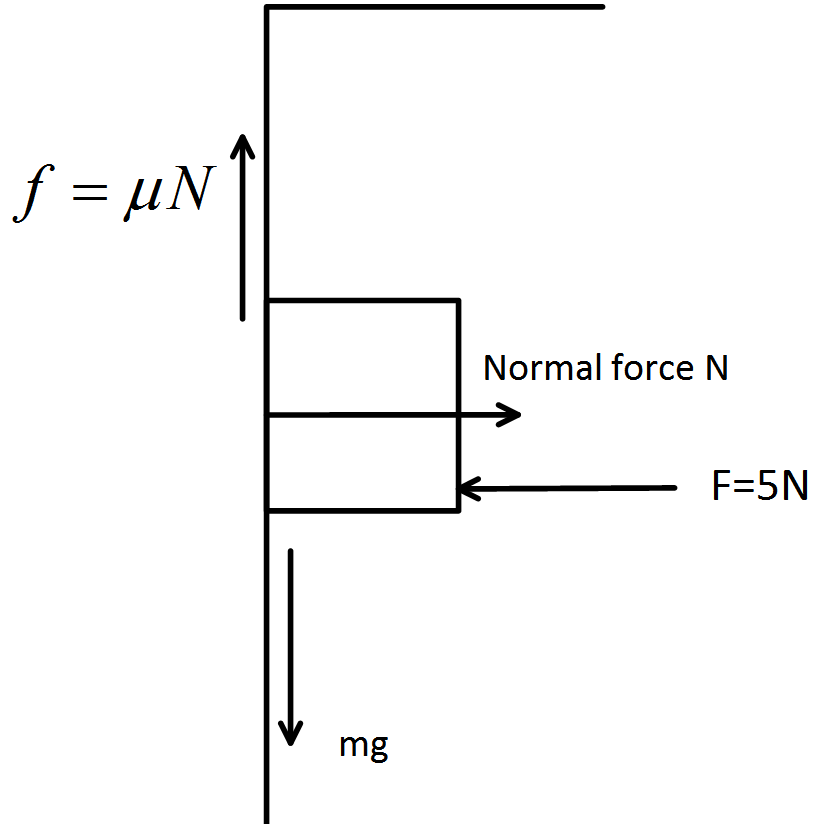
Now, we can see that, ${f_{\max }} > mg$ . If there is a net force then there will be motion of the block but here that is not possible. Here, the static frictional force must be equal to the weight or the gravitational pull.
So, the frictional force acting on the body must be equal to the weight of the body.
Hence, frictional force acting on the body is $0.98N$ .

Note :
Here we can see that frictional force has a larger available value but frictional force acting on it is different. So, how is that possible?. Actually, the static coefficient of friction actually takes a suitable value between $0 < {\mu _s} < 0.5$ to balance the force.