Solveeit Logo
Login

Question

Question: A block of ice at temperature \( - 20^\circ {\rm{C}}\) is slowly heated and converted to steam at \(...

A block of ice at temperature −20∘C - 20^\circ {\rm{C}} is slowly heated and converted to steam at 100∘C100^\circ {\rm{C}}. Which of the following diagrams is most appropriate?

Explanation

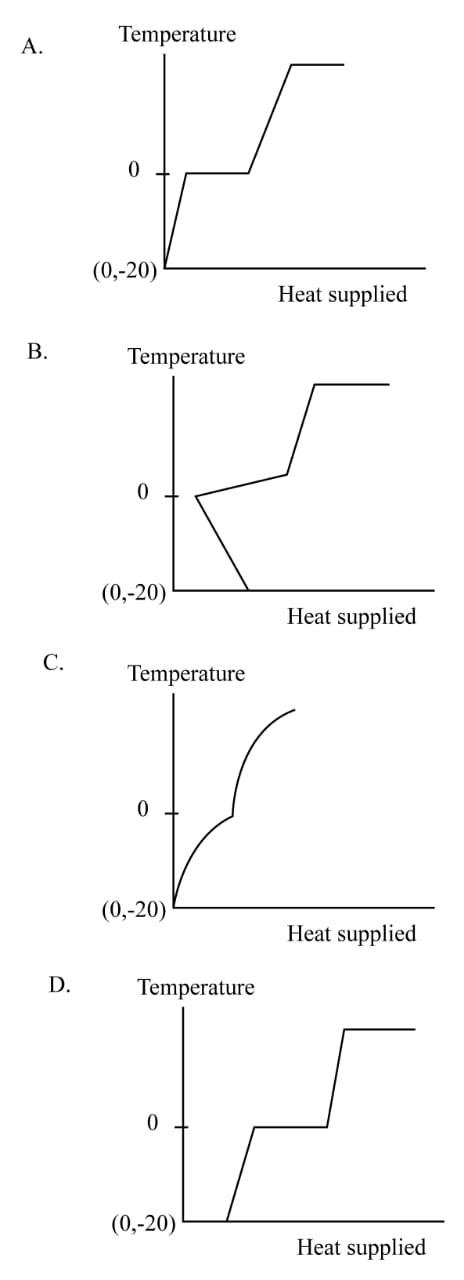
Solution

Here we use the concept of latent heat of fusion and vaporization. The amount of heat required to change the state of the substance without any change in its temperature is known as the latent heat of a substance.

Complete step by step answer:
In this problem, the temperature of ice first will increase from −20∘C - 20^\circ {\rm{C}} to 0∘C0^\circ {\rm{C}}.
The heat supplied for this process will be
∴Q1=msiΔT\therefore {Q_1} = m{s_i}\Delta T
Here, Q1{Q_1} is the heat applied, m is the mass of ice, si{s_i} is the specific heat of solid ice and ΔT\Delta T is the change in temperature which is from −20∘C - 20^\circ {\rm{C}} to 0∘C0^\circ {\rm{C}}.
Therefore the ice starts melting and the temperature during melting remains constant at 0∘C0^\circ {\rm{C}}.
Now the heat supplied in this process will be
∴Q2=mLf\therefore {Q_2} = m{L_f}
Where m is the mass of ice, Lf is the latent heat of melting.
Now the temperature of water will increase from 0∘C0^\circ {\rm{C}}to 100∘C100^\circ {\rm{C}}.
∴\therefore Heat supplied Q3{Q_3} will be
⇒Q3=mswΔT1\Rightarrow {Q_3} = m{s_w}\Delta {T_1}
Where sw{s_w} is the specific heat of water, ΔT1\Delta {T_1} is the change in temperature of the water from 0∘C0^\circ {\rm{C}} to 100∘C100^\circ {\rm{C}}.
Finally, water at 100∘C100^\circ {\rm{C}} will be converted into steam at 100∘C100^\circ {\rm{C}}, and during this process, the temperature remains constant. The temperature versus heat supplied graph is shown in the figure:

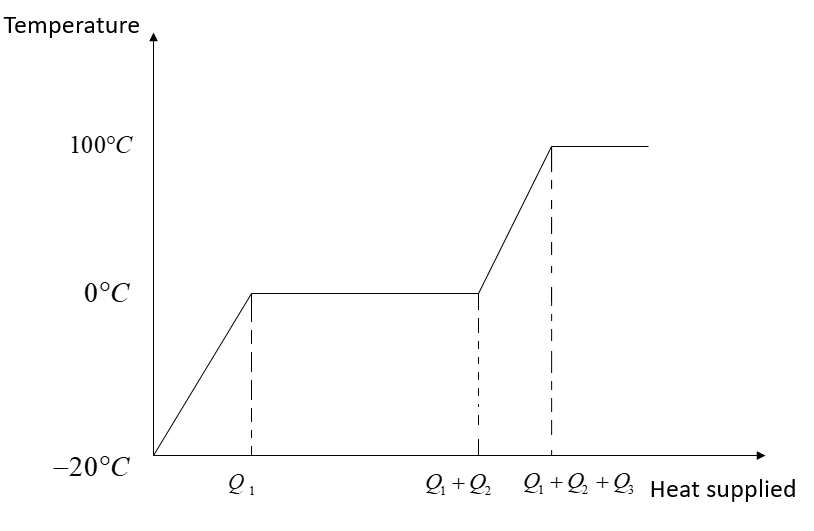
Therefore, the most appropriate figure mentioned in option (A). Hence the correct option is (A).

Additional information:
When water freezes into ice, heat energy is released. Since the latent heat of fusion of ice is 80cal/g80cal/g. That is why the atmosphere remains warm during snowfall. Water is the base of both ice and steam. When ice turns directly into the water without transitioning into a liquid, this phase is called sublimation.

Note:
We can go wrong by assuming that there is a temperature change while phase change but in reality, there is no temperature change during phase change, and all the heat required to change the state from solid ice at 0 degrees Celsius to water at 0 degrees Celsius.