Question

A block of brass of mass 0.5kg and density $8\times {{10}^{3}}Kg/{{m}^{3}}$ is suspended from a string. What will be the tension in the string if the block is completely immersed in water? (g=10 m/s$^{2}$)

Answer 1

At first draw the diagram for the question given, then find the relation between apparent weight and tension of the string, write the formula for apparent weight and find the volume of water displaced by the block. Then calculate the apparent weight of the block. This weight will be the weight that is acting on the string when the block is immersed in water.

Complete answer:
Here in this diagram, we see that a block is immersed in a water bath, and tension ‘T’ is acting on the string by which the block is attached to a fixed rigid surface.

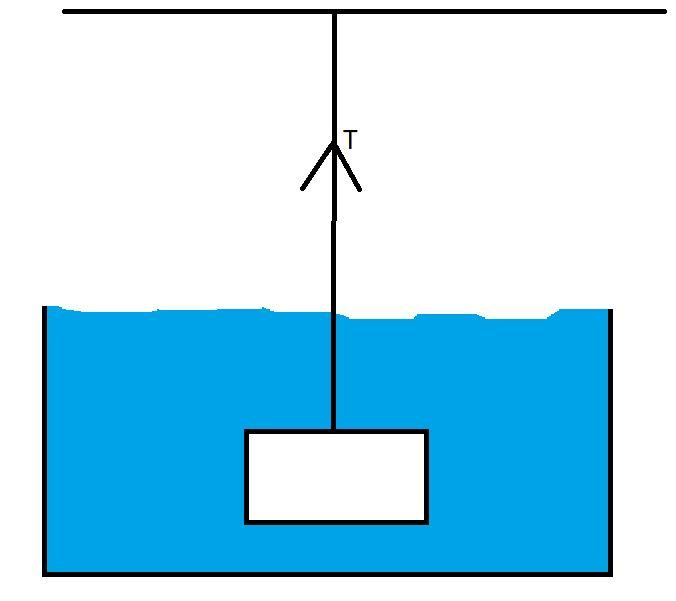
Now we can say that the string with tension ‘T’ would counterbalance the actual weight of the block if it was not immersed.

So now, tension ‘T’ is balancing the apparent weight of the block.
Now to find the apparent weight we know that apparent weight is,
AW = True Weight – Weight of liquid displaced.
To find the weight of the liquid displaced, we have to find the volume,
We know that volume V = M / D, where M is the mass, and D is the density.

So, volume of the block (V)=$\dfrac{0.5}{8\times {{10}^{3}}}{{m}^{3}}$
V= $\dfrac{5}{8}\times {{10}^{-4}}{{m}^{3}}$.
Now,
$AW=\text{ }0.5~\times 10\dfrac{5}{8}\times {{10}^{-4}}\times {{10}^{3}}\times 10$
$AW=\left( 5-\dfrac{5}{8} \right)$ ,
AW=4.37 N,
This is the weight that the string is counterbalancing, that is the tension of the string is 4.37N.

Note:
When calculating the volume of water displaced by the block we also need to multiply it with the density of water and the gravitational pull of the earth that is given as (g). We must notice that the weight of the block is the tension acting on the string.