Question

A block of base $10cm\times 10cm$and height 15cm is kept on an inclined plane. The coefficient of friction between them is $\sqrt{3}$. The inclination $\theta$ of this inclined plane from the horizontal plane is gradually increased from ${{0}^{\circ }}$. Then:
a) at $\theta ={{30}^{\circ }}$, the block will start sliding down the plane
b) The block will remain at rest on the plane up to certain $\theta$and then it will topple
c)at $\theta ={{60}^{\circ }}$, the block will start sliding down the plane and continue to do so at higher angles
d) at $\theta ={{60}^{\circ }}$, the block will start sliding down the plane and further increasing $\theta$it will topple at certain at certain $\theta$

Answer 1

In the above question the coefficient of friction the block and the horizontal plane is given to us. Hence we will first draw the free body diagram of the above scenario. Further we will obtain the condition for sliding and toppling at a particular inclination and select the correct alternative from those provided.

Complete answer:
The diagram represents the free body diagram of the block with mass m.

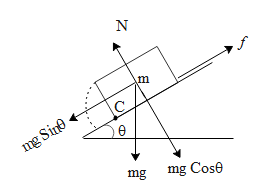
First let us discuss the sliding phenomenon of the block. The sliding of the above block will be observed, if the component of the gravitational force i.e. $mgSin\theta$ is greater than the force of friction (f) which holds the block from moving down along the inclined plane. The force of friction is given as the product of the normal force (N) times the coefficient of friction ($\mu$). Mathematically this can be written as,
$\begin{aligned} & f=\mu N \\\ & \because \mu =\sqrt{3}\text{ and N=}mgCos\theta \\\ & \Rightarrow f=\sqrt{3}mgCos\theta \\\ \end{aligned}$
If the component of gravity along the plane increases then the frictional force, the block will slide. Hence we can write condition for sliding as,
$\begin{aligned} & f=mgSin\theta \\\ & \Rightarrow \sqrt{3}mgCos\theta =mgSin\theta \\\ & \Rightarrow \dfrac{Sin\theta }{Cos\theta }=\sqrt{3}\text{, }\because \dfrac{Sin\theta }{Cos\theta }=\tan \theta \\\ & \Rightarrow \tan \theta =\sqrt{3} \\\ & \Rightarrow \theta ={{60}^{\circ }} \\\ \end{aligned}$
Therefore we can conclude that if the angle of inclination is increased by more than 60 degrees the block will start sliding down.
Now let us discuss the toppling effect of the block i.e. rotation of the block about the axis passing through one of its points.
In the above free body diagram we can see that for a particular value of $\theta$ the block will topple along the point C such that the dotted line depicts the path followed while toppling by the centre of mass. Torque ($\tau$)about the axis of rotation is defined as the perpendicular distance(r) from the axis times the force (F)acting tangentially to the radius vector i.e. perpendicular distance. Mathematically this can be written as, $\tau =Fr$
If we see the above diagram, The normal force and the frictional force are contact forces and while the block topples, the point C will only be in contact. Since r for the above two forces are zero we can say that the torques due to frictional and normal force will be zero. But both the components of gravity will generate torques about the centre of mass.
The length of the base along both the sides is given as 10cm. hence the component of gravity i.e. $mgCos\theta$ will lie at a distance of 5cm from point C. Similarly the height of the block is given as 15 cm. hence the component of gravity i.e. $mgSin\theta$ will lie at a distance of 7.5cm from the point C. The torque due to both the components should be equal in order to block at a stable position. Hence equating the torques due to them we get,
$\begin{aligned} & \tau (mgSin\theta )=\tau (mgCos\theta ) \\\ & \Rightarrow mgSin\theta \times 7.5=mgCos\theta \times 5 \\\ & \Rightarrow \tan \theta =1/15 \\\ & \Rightarrow \theta ={{33.66}^{\circ }} \\\ \end{aligned}$
As we keep on increasing the angle, at $\theta >{{33.66}^{\circ }}$ the block will topple.

So, the correct answer is “Option B”.

Note:
In the above solution we obtained that the block will start sliding at 60 degrees. But before that itself the block topples at an angle of 33.66 degrees. Hence we could say that the block topples at an angle $\theta$ with respect to the horizontal plane.