Question

A block $M$ hangs vertically at the bottom end of a uniform rope of constant mass per unit length. The top end of the rope is attached to a fixed rigid support at $O$. A transverse wave pulse (pulse 1) of wavelength ${\lambda _0}$ is produced at point $O$ on the rope. The pulse takes time ${T_{OA}}$ to reach point $A$. If the wave pulse of wavelength ${\lambda _0}$ is produced at point $A$ (pulse $2$) without disturbing the position of $M$ it takes time ${T_{AO}}$ to reach point $O$. Which of the following options is/are correct?

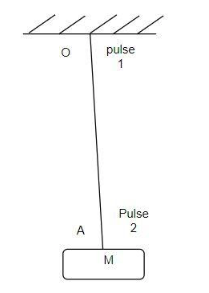
(A) The time ${T_{OA}} = {T_{AO}}$
(B) The velocities of the two pulses (pulse $1$ and pulse $2$ ) are the same at the midpoint of rope.
(C) The wavelength of pulse $1$ becomes longer when it reaches point $A$.
(D) The velocity of any pulse along the rope is independent of its frequency and wavelength.

Answer 1

When the string is hanged from the fixed support with a mass, then the force acting on it and its transmission mainly depends upon the tension of the string. The wavelength produced in the one end passes to the other end by the vibration.

Useful formula:
The speed of the wave is given by
$v = \sqrt {\dfrac{T}{\mu }}$
Where $v$ is the speed of the wave, $T$ is the tension along the thread and $\mu$ is the mass per unit length of the suspending string.

Complete step by step solution:
The speed of the vibration that passes through the string depends on the tension in the string.
$v = \sqrt {\dfrac{T}{\mu }}$
The tension is the same for a massless string hence, ${T_{OA}} = {T_{AO}}$.
Thus the option (A) is correct.
The velocity remains constant since it depends on tension and it is clear that the velocity is the same at the midpoint of the rope. Thus the option (B) is also correct.
The wavelength depends on the frequency and the velocity. Since the frequency and the velocity is constant at all parts of the string, wavelength is also constant. Thus option (C) is incorrect.
But the velocity depends only on the tension of the string not frequency and wavelength. Thus option (D) is also correct.

Thus, the option (A), (B) and (D) are correct.

Note: Tension is the pulling force and it is constant in the string where it has the negligible mass. This is because it follows Newton's third law. For every action there is an equal and the opposite reaction, for every change in the tension there will be opposite pull.