Question

A block is released from the top of a smooth hemisphere to slide down along its surface. At what angle $\theta$, will the block leave contact with the hemisphere?

A. ${\cos ^{ - 1}}\left( {\dfrac{1}{3}} \right)$
B. ${\cos ^{ - 1}}\left( {\dfrac{2}{3}} \right)$
C. ${\cos ^{ - 1}}\left( {\dfrac{1}{4}} \right)$
D. ${\cos ^{ - 1}}\left( {\dfrac{3}{4}} \right)$

Answer 1

First, draw a diagram by assigning the forces acting on the block. Then form an equation by balancing the forces. You will need to use here conservation energy, so recall the concept of conservation of energy. Find the total energy of the block when it is at rest and when the block leaves the contact of the hemisphere. Use these values to find the value of $\theta$.

Complete step by step answer:
Given, a block is released from the top of a smooth hemisphere, slides down and at a point it leaves the contact with the hemisphere. Radius of the hemisphere, $R$. Let $m$ be the mass of the block and $v$ be the velocity with which it slides. Let $g$ be acceleration due to gravity.And let Y be the point where the block leaves the hemisphere. We draw the figure by assigning the forces acting on the block.

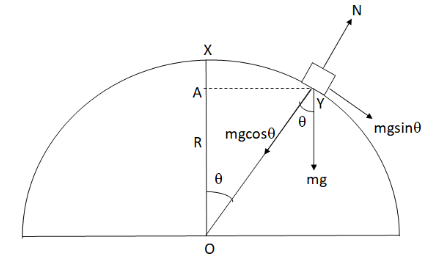
In the figure, $N$ is the normal reaction.
When the block slides down the hemisphere will experience a centripetal force towards the point O.
The formula for centripetal force is,
$C.F = \dfrac{{m{v^2}}}{R}$
The centripetal force acts radial direction towards the centre that is here it will act towards O, so from the diagram we have,
$mg\cos \theta - N = \dfrac{{m{v^2}}}{R}$ (i)
According to conservation of energy, at all points the sum of kinetic and potential energies is the same. That is, at point X and point Y the sum of kinetic and potential energies of the block will be the same.
The potential energy of a object at a height $h$ is given by,
$P.E = mgh$ (ii)
The kinetic energy of a object with speed $v$ is given by,
$K.E = \dfrac{1}{2}m{v^2}$ (iii)
For point X,
The height is OX that is $R$. So potential energy using equation (ii) we get,
${\left( {P.E} \right)_X} = mgR$
At point X, the block is at rest so kinetic energy is zero.
Therefore, sum of kinetic and potential energy at point X is,
${E_X} = mgR + 0 = mgR$ (iv)
For point Y,
The height is OA which is $R\cos \theta$ so the potential energy using equation (ii) we get
${\left( {P.E} \right)_Y} = mgR\cos \theta$
The kinetic energy at point Y using equation (iii) we get,
${\left( {K.E} \right)_Y} = \dfrac{1}{2}m{v^2}$
Therefore, the sum of kinetic and potential energies at point Y is,
${E_Y} = \dfrac{1}{2}m{v^2} + mgR\cos \theta$ (v)
Using conservation of energy and equating equation (iv) and (v) we get,
${E_X} = {E_Y}$
Putting the values of ${E_X}$ and ${E_Y}$ we get,
$mgR = \dfrac{1}{2}m{v^2} + mgR\cos \theta$
$\Rightarrow mgR - mgR\cos \theta = \dfrac{1}{2}m{v^2}$
$\Rightarrow 2\left( {mg - mg\cos \theta } \right) = \dfrac{{m{v^2}}}{R}$
$\Rightarrow \dfrac{{m{v^2}}}{R} = 2\left( {mg - mg\cos \theta } \right)$
Substituting the value of $\dfrac{{m{v^2}}}{R}$ in equation (i), we get
$mg\cos \theta - N = 2\left( {mg - mg\cos \theta } \right)$
$\Rightarrow mg\cos \theta + 2mg\cos \theta = 2mg + N$
$\Rightarrow 3mg\cos \theta = 2mg + N$
$\Rightarrow 3\cos \theta = 2 + \dfrac{N}{{mg}}$
$\Rightarrow 3\cos \theta - 2 = \dfrac{N}{{mg}}$ (vi)
When the block leaves the contact of the hemisphere then the normal reaction will vanish, that is $N = 0$. Putting this value in equation (vi) , we get
$3\cos \theta - 2 = 0$
$\Rightarrow 3\cos \theta = 2$
$\Rightarrow \cos \theta = \dfrac{2}{3}$
$\therefore \theta = {\cos ^{ - 1}}\left( {\dfrac{2}{3}} \right)$
Therefore, the angle at which the block leaves the contact of the hemisphere is ${\cos ^{ - 1}}\left( {\dfrac{2}{3}} \right)$.

Hence, the correct answer is option B.

Note: There are four important conservation laws that one should always remember, which are conservation of energy, conservation of linear momentum, conservation of angular momentum and conservation electric charge. These laws are applicable for any system, that is we can use them in any system.