Question

A block is placed over a large plank (plank is kept on horizontal surface). The coefficient of friction between the block and the plank is $\mu = 0.2$.Initially both are at rest, suddenly the plank starts moving horizontally with acceleration ${a_0} = 4m/{s^2}$with the help of some external force. The displacement of the block in $1s$ is $(g = 10m/{s^2})$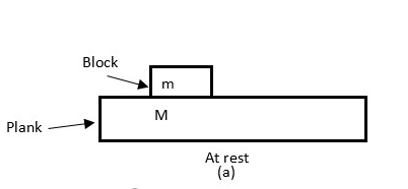
A. $1m\,$relative to ground
B. $1m$relative to plank
C. Zero relative to plank
D. $2m\,$relative to ground

Answer 1

Concept of force and equation of motion and frictional force. As the plank moves forward due to external force, the block will move backward with respect to plank.

Formula used:
$s = ut + \dfrac{1}{2}a{t^2} \\\ f = \mu R \\\$

Complete answer:
Let us consider the plank of mass M and block of mass m.
Initially, as shown in figure (a) both are at rest.
I.e. $at\,t = 0,4 = 0\,and\,\mu = 0.2$
But after sometime, plank moves with an acceleration of $4m/{s^2}.$
Considering the motion of block w.r.t plank as shown in figure (b) we have
$4m-\mu R = ma ...(i)$
Where a is the net acceleration experience by block of mass m.
Now, reaction R balances the weight of the block.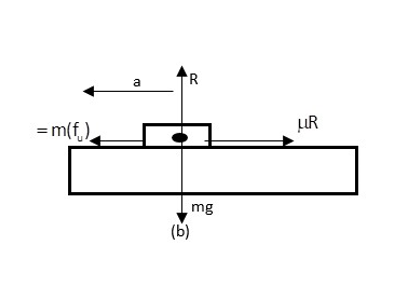
So, $R = mg$
Hence, equation (i) becomes
$4m - \mu mg = ma \\\ m(4 - \mu g) = ma \\\ \Rightarrow 4 - \mu g = a \\\$
As g $=$ acceleration due to gravity
$= 10m/{s^2}$
And $\mu =$coefficient of friction $= 0.2$
$\Rightarrow a = 4 - \mu g \\\ \Rightarrow a = 4 - (0.2)(10) \\\$
So, acceleration becomes
$a = 4 - 2 \\\ a = 2m/{s^2} \\\$
Now, using equation of motion
$s = u{t^2} + \dfrac{1}{2}a{t^2} …………...(ii)$
We know,
$u = 0\,m/{s^2} \\\ a = 2\,m/{s^2} \\\ t = 1\,\sec \\\$
So, equation (ii) becomes
$s = 0(1) + \dfrac{1}{2} \times 2 \times {(1)^2}$
$s = 1m,\,relative\,\,to\,\,plank$

So, the correct answer is “Option B”.

Note:
Here we have to solve in order to get resultant force. We have taken $u = 0$ as initially both plank and block are at rest and as block moves due to acceleration of plank, $1m$ is displacement w.r.t plank.