Question

A block is moving on an inclined plane making an angle ${45^ \circ }$ with the horizontal and coefficient of friction is $\mu$. The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down. If we define $N = 10\mu$, then N is –
A. 2
B. 3
C. 4
D. 5

Answer 1

This problem can be solved by drawing the free-body diagram, which is the diagram of the body which includes all the forces acting in the body. Then, the forces in the horizontal and vertical directions must be equated to find the unknown force.
Frictional force is the obstruction offered to the relative motion of the body over a surface by the virtue of the surface on which a body is moving.

Complete step-by-step answer:
The frictional force is directly proportional to the normal force exerted by the surface on the body. The expression for frictional force is:
$f = \mu N$
where $\mu$= coefficient of friction and N = normal force.
Consider the free-body diagram of a block moving on an inclined plane making an angle of ${45^ \circ }$ with the horizontal when it is in equilibrium.

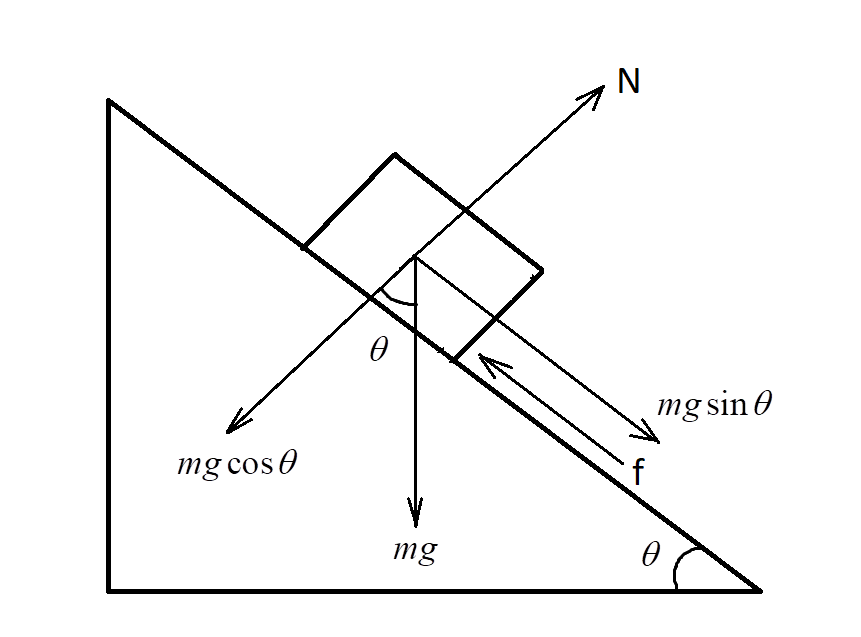
The weight of the object W = mg, acts vertically downwards and the normal acts in the direction perpendicular to the inclined plane as shown in the figure. The components of weight are also shown in the figure.
There are two kinds of forces independently acting on the block, due to the motion of the block. i) ${F_1}$ : This force applied to prevent the sliding of the block. ii) ${F_2}$: This force pushes the block upwards.

The relationship among these forces as given in the question:
${F_2} = 3{F_1}$
Let us calculate the values of these forces.
To calculate ${F_1}$:
Let us draw the free-body diagram for this case.

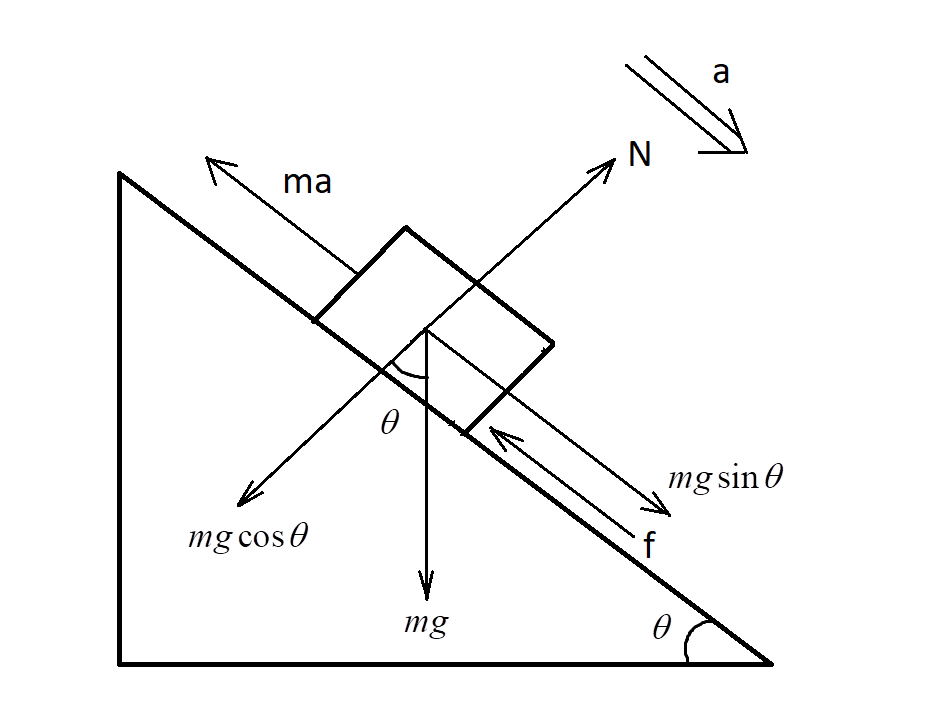
The block is trying to slide down. Hence, the direction of the acceleration is downwards.
The force equal to mass times the acceleration acts in the opposite direction preventing the sliding down of the block, which is equal to ma.
By equating the forces in the above figure:
$N = mg\cos \theta$
${F_1} = mg\sin \theta - f$
The frictional force, $f = \mu N = \mu mg\cos \theta$
Substituting, we get –
${F_1} = mg\sin \theta - \mu mg\cos \theta$

To calculate ${F_2}$:
Let us draw the free-body diagram for this case.

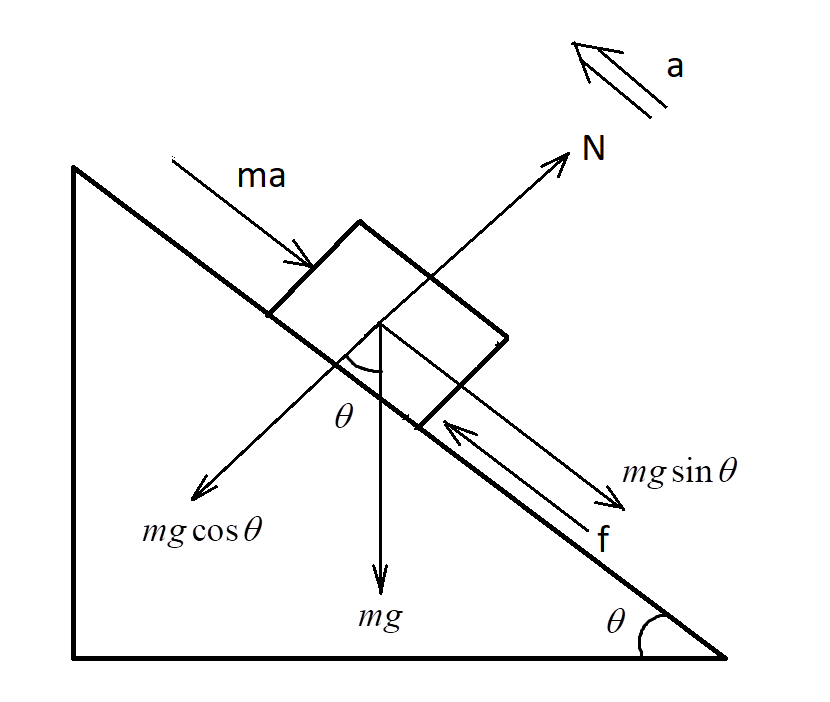
The block is being pushed upwards. Hence, the direction of the acceleration is upwards.
The force equal to mass times the acceleration acts in the opposite direction, pushing the block above the plane.
By equating the forces in the above figure:
$N = mg\cos \theta$
${F_2} = mg\sin \theta + f$
The frictional force, $f = \mu N = \mu mg\cos \theta$
Substituting, we get –
${F_2} = mg\sin \theta + \mu mg\cos \theta$
Given the relation, ${F_2} = 3{F_1}$
Substituting the values, we get –
$mg\sin \theta + \mu mg\cos \theta = 3\left( {mg\sin \theta - \mu mg\cos \theta } \right)$
$\Rightarrow mg\sin \theta + \mu mg\cos \theta = 3mg\sin \theta - 3\mu mg\cos \theta$
$\Rightarrow 2mg\sin \theta = 4\mu mg\cos \theta$
$\Rightarrow \mu = \dfrac{2}{4} \times \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{1}{2}\tan \theta$

The inclined plane is at an angle of ${45^ \circ }$ to the horizontal.
$\theta = {45^ \circ } \Rightarrow \tan \theta = 1$
Substituting,
$\mu = \dfrac{1}{2} \times 1 = \dfrac{1}{2}$
The relationship between the normal and the coefficient is given by – $N = 10\mu$
Hence, $N = 10 \times \dfrac{1}{2} = 5$

Therefore, the correct option is Option D.

Note: Students generally, confuse while writing the horizontal and vertical components of a vector. You can use a simple and handy thumb rule.