Question

A block is kept on a frictionless inclined surface with angle of inclination $\theta$. The incline is given an acceleration $a$ to keep the block stationary. Then $a$ is equal to (take acceleration due to gravity $= g$)

(A) $\dfrac{g}{{\tan \theta }}$
(B) $g{\text{ cosec}}\theta$
(C) $g$
(D) $g{\text{ tan}}\theta$

Answer 1

For the block to appear constant relative to the block, the force pulling the block must create an acceleration which would balance the acceleration due to the weight component of the body. The horizontal force on the block can be modelled according to Newton’s second law.
Formula used: In this solution we will be using the following formulae;
$W = mg$ where $W$ is the weight of a body, $m$ is the mass, and $g$ is acceleration due to gravity.
$F = ma$ where $F$ is the force acting on a body, and $a$ is the net acceleration of the body.

Complete Step-by-Step solution:

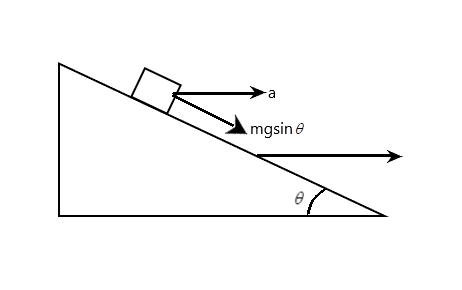
For the block to appear constant relative to the block, the force pulling the block must create an acceleration which would balance the acceleration due to the weight component of the body.
Now, the weight component of the body is simply
${W_p} = W\sin \theta = mg\sin \theta$ since ($W = mg$ where $W$ is the weight of a body, $m$ is the mass, and $g$ is acceleration due to gravity).
Now, the acceleration of the entire wedge is shown to be horizontal. The force acting on the block due to this force causing the acceleration would be given from newton’s law (which is$F = ma$ where $F$ is the force acting on a body, and $a$ is the net acceleration of the body) as
${F_b} = ma$
Now, the component of the force in the same direction as the weight component is
${F_p} = ma\cos \theta$
Since, they must be equal, we have
$mg\sin \theta = ma\cos \theta$
Hence,
$a = g\dfrac{{\sin \theta }}{{\cos \theta }} = g\tan \theta$

The correct option is D

Note: For clarity, the acceleration points in the same direction as the weight component because, if the wedge is moved forward, due to inertia, the block is though it’ll move backward. This backward fictitious force is equal to the real forward force acting on the wedge.