Question
Question: A block is in equilibrium. The tension in the string is \(\left( {\mu < \tan \theta } \right)\) 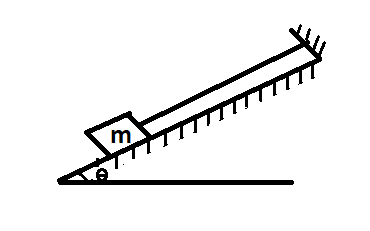
A. mg(sinθ−μcosθ)
B. mg(sinθ+μcosθ)
C. mgsinθ
D. Zero
Solution
It is given in the question that the block is in equilibrium. An object will be at equilibrium when the linear momentum of its center of mass and the angular momentum about its center of mass will be constant. Here, we will resolve the weight mg of the block to calculate the tension in the string.
Complete step by step answer:
Consider a block of mass m which is attached to a rigid support. This block is placed on an inclined plane which is making an angle θ with the surface. Let mg be the weight of the block.
Now, if we resolve the weight mg of the block into two components
mgcosθ which is perpendicular to the plane of the block.
mgsinθ which is along the plane of the block.
Now, the force along the inclined plane will be zero. Also, the force which is perpendicular to the inclined plane is also zero.
Now, let us denote the force in the upward direction of the mass m as N .
Therefore, for the direction of friction, the tendency of the motion of block is given by
N=mgcosθ
Now, if we cut the wire with which the block is attached to a rigid support. Therefore, the mass will move downward due to gravity.
Now, the tendency of the relative motion is μN and it is opposite to the acceleration due to gravity.
Therefore, the tension T in the block is given by
T=mgsinθ−μmgcosθ
⇒T=mg(sinθ−μcosθ)
Therefore, the tension in the string is mg(sinθ−μcosθ) .
So, the correct answer is “Option A”.
Note:
When the system will be in equilibrium, therefore, the tension in the string will be pointed away from the mass, that is, in the direction of the string.
When the system will be in equilibrium, the sum of all the forces will be zero.
⇒∑F=0
