Question
Question: A block is given a speed u up the inclined plane as shown. Using the work energy theorem, find out X...
A block is given a speed u up the inclined plane as shown. Using the work energy theorem, find out X, when the block stops moving.
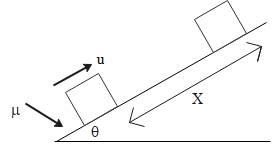
Solution
Hint: According to the work energy theorem, the total work done by the system is equal to the change in kinetic energy of the system. The work done here is against gravity and the friction force of the surface to move the box from one position to another.
Complete step-by-step answer:
We are given a box. Let its mass be m kgs. It is given a speed up the inclined plane. Therefore, the initial velocity of the box is u. Since, the box eventually comes to rest after traveling a distance x, its final velocity is zero. Therefore, v = 0 and final kinetic energy is also zero. Hence, change in kinetic energy is given as
ΔK=21mv2−21mu2 =0−21mu2=−21mu2 ...(i)
Now the various forces acting on the box are as follows:
1. The force due to gravity. If we resolve the components of weight mg, the component acting along the inclined plane is
Wg=−mgsinθ ...(ii).
2. The force due to friction. The distance travelled by box before coming to rest is X. Therefore the frictional force acting on the box is given as
Wf=−μmgxcosθ ...(iii)
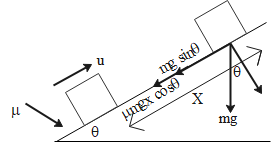
Now, according to the work energy theorem, the total work done by a system is equal to the change in its kinetic energy. Therefore, with the available information we can write the work energy theorem for box’s motion as follows.
Wg+Wf=ΔK
Substituting the equation (i), (ii) and (iii), we get
\-mgsinθ−μmgxsinθ=−21mu2 ⇒μmgxcosθ=21mu2−mgsinθ ⇒x=μmgcosθ1(21mu2−mgsinθ)
Solving further, we get
x=2g(sinθ+μcosθ)u2
This is the required value of X.
Note: The two forces, one due to gravity and other due to friction, are trying to stop the motion of the box i.e. they are acting in opposite directions of the motion of the box, due to which their magnitude are taken to be negative.
