Question

A block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in the figure. The horizontal velocity of the block is:

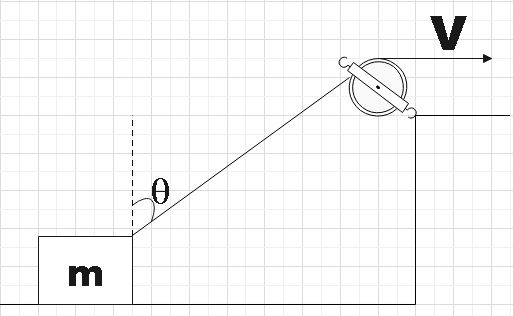
A. v
B. $\dfrac{v}{\sin \theta }$
C. $v\sin \theta$
D. $\dfrac{v}{\cos \theta }$

Answer 1

As a first step you could redraw the mass-pulley system by marking the horizontal and vertical distance. Then you could apply the Pythagorean theorem and then differentiate on both sides with respect to time. Therefore, you will be able to get the horizontal velocity of the block as given in the options.

Complete step-by-step solution:
In the question we are given a situation where a block is being dragged by virtue of a rope with velocity v. We are asked to find the horizontal velocity v’ of the block.

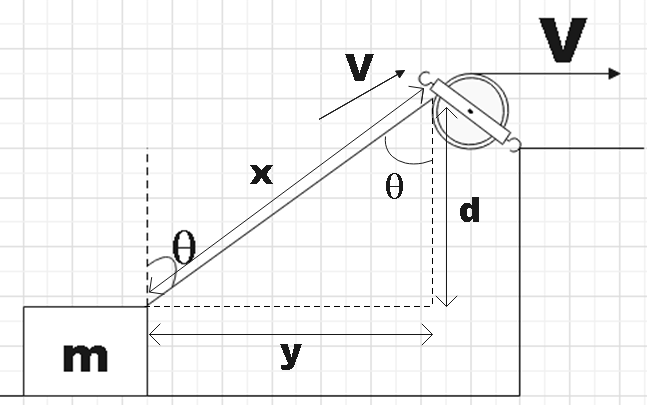
On applying Pythagorean theorem in the above triangle we get,
${{x}^{2}}={{y}^{2}}+{{d}^{2}}$
Now, we could differentiate on both sides with respect to time to get,
$2x\dfrac{dx}{dt}=2y\dfrac{dy}{dt}+0$ ………………………………………………….. (1)
From the figure we see that time rate of change of y is horizontal velocity of the block to be found,
$\dfrac{dy}{dt}=v'$
But from (1) we have,
$v'=\dfrac{2x}{2y}\dfrac{dx}{dt}=\dfrac{x}{y}v$ …………………………….. (2)
Where v is the velocity at which the rope is moving. Now from the figure we have,
$\sin \theta =\dfrac{y}{x}$
Therefore, equation (2) now becomes,
$v'=\dfrac{v}{\sin \theta }$
Hence, option B is the correct answer.

Note: In the figure we see that the distance d doesn’t change with time. ‘d’ is the distance between the top of the block from the pulley and that remains constant as there is no vertical displacement for the block. And therefore we get 0 on differentiating d with respect to time as given in equation (1).