Question

A block having a mass $m$ is pulled by applying a force at an angle $\theta$ with the horizontal along a horizontal surface. Let us assume that the block travels with a uniform velocity and is having a displacement $d$ and the coefficient of friction is $\mu$, therefore the work done by the applied force can be written as,
$\begin{aligned} & A.\dfrac{\mu mgd}{\cos \theta +\mu \sin \theta } \\\ & B.\dfrac{\mu mgd\cos \theta }{\cos \theta +\mu \sin \theta } \\\ & C.\dfrac{\mu mgd\sin \theta }{\cos \theta +\mu \sin \theta } \\\ & D.\dfrac{\mu mgd\cos \theta }{\cos \theta -\mu \sin \theta } \\\ \end{aligned}$

Answer 1

The balancing of the force acting on the body is to be found first. This is to be found both in the horizontal as well as vertical direction. From this find out the external force acting on the body. Using this calculate the work done by the applied force on the block. This information will help you to solve this question.

Complete step by step answer:

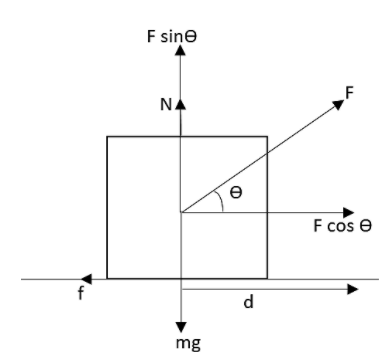
From the figure we can write that the total force acting on the block is balanced as it is in equilibrium.
In vertical direction we can write that,
$N+F\sin \theta =mg$
Where $N$be the normal force acting on the body, $\theta$ be the angle at which force acts, $F$ be the force applied on the block, $g$ be the acceleration due to gravity and $m$ be the mass of the particle.
The equation can be rewritten as,
$N=mg-F\sin \theta$
In the horizontal direction, we can see that the block is moving with a fixed velocity. Therefore the cosine component of the force is balanced by the frictional force $f$. That is,
$f=F\cos \theta$
The friction is given by the equation,
$f=\mu N$
Substituting this in the equation will give,
$\mu N=F\cos \theta$
The normal force can be substituted by the equation we obtained above. That is,

& \mu \left( mg-F\sin \theta \right)=F\cos \theta \\\ & \Rightarrow F=\dfrac{\mu mg}{\cos \theta +\mu \sin \theta } \\\ \end{aligned}$$ The work done by the external force can be obtained as, $$W=F\cdot S$$ Where $$S$$be the displacement of the block given as, $$S=d\cos \theta $$ Therefore the work done will be, $$W=\dfrac{\mu mgd\cos \theta }{\cos \theta +\mu \sin \theta }$$ **The answer is mentioned as option B.** **Note:** The work done is defined as the amount of energy dissipated when there is a displacement occurring due to an external force acting. Work is expressed in the units of joule. The work done is a scalar quantity which is not dependable on the direction.