Question

A block has dimensions and. Ratio of maximum resistance to minimum resistance between any pair of opposite faces of the block is:
(a) 9 : 1
(b) 1 : 9
(c) 18 : 1
(d) 1 : 6

Answer 1

In this solution, we are going to use the formula of resistance that shows the relationship of Resistance with length and area. We must know that, Resistance of any conductor is directly proportional to its length and inversely proportional to its area.

Complete Step by Step Answer: Given:
Dimensions of block are:

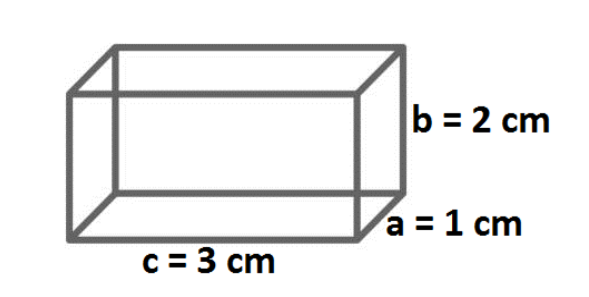
$a = 1$cm,
$b = 2$cm, and
$c = 3$cm
We get maximum resistance ${R_{\max }}$ when the length of conductor$\left( l \right)$is maximum and Area of cross-section$\left( A \right)$is minimum.
Similarly, for minimum resistance${R_{\min }}$the length of conductor$(l)$should be minimum and area of cross-section$\left( A \right)$is maximum.
From the given dimensions of the block:
Maximum length:
${l_{\max }} = c \\\ = 3\;cm \\\$
Minimum length:
${l_{\min }} = a \\\ = 1\;cm \\\$
Maximum area of cross-section:
${A_{\max }} = b \times c \\\ {A_{\max }} = 2 \times 3 \\\ {A_{\max }} = 6\;c{m^2} \\\$
Minimum area of cross-section:
${A_{\min }} = a \times b \\\ {A_{\min }} = 1 \times 2 \\\ {A_{\min }} = 2\;c{m^2} \\\$
The formula to calculate resistance $R$is given by:
$R = \rho \dfrac{l}{A}\;\;\;..........(1)$
Where $\rho$ is the resistivity of the block. The value of resistivity is constant for a material.
$l$ is length of conductor, and$A$is area of cross-section.
Now, substituting values of ${l_{\min }}$and ${A_{\max }}$ in Equation (1), to get${R_{\min }}$:
${R_{\min }} = \rho \dfrac{{{l_{\min }}}}{{{A_{\max }}}}\;\;\; \\\ {R_{\min }} = \rho \dfrac{1}{6}\;\;\;\;.......(2) \\\$
And, substituting the value of ${l_{\max }}$ and ${A_{\min }}$ in Equation (1), to get${R_{\max }}$:
${R_{\max }} = \rho \dfrac{{{l_{\max }}}}{{{A_{\min }}}}\;\;\; \\\ {R_{\max }} = \rho \dfrac{3}{2}\;\;\;\;.......(3) \\\$
Dividing equation (3) with equation (2), we get,

$$\dfrac{{{R_{\max }}}}{{{R_{\min }}}} = \dfrac{{\rho \dfrac{3}{2}\;}}{{\rho \dfrac{1}{6}\;}} \\\ \dfrac{{{R_{\max }}}}{{{R_{\min }}}} = \dfrac{9}{1} \\\$$

Therefore, the ratio of maximum resistance to minimum resistance between any pair of opposite faces of the block is 9 : 1.
So option (a) is the correct answer.

Note: While substituting the values of $l$ (length of conductor) and $A$(area of cross-section) you don’t need to convert the values into its S.I units because as we are calculating the ratio, the corresponding units get cancelled out. Also, make sure that you calculate the ratio of maximum resistance to minimum resistance and not the minimum resistance to maximum resistance.