Question

A block has been placed on an inclined plane. The slope angle $\theta$ of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is equal to
(A) $\sin \theta$
(B) $\cos \theta$
(C) $\sec \theta$
(D) $\tan \theta$

Answer 1

We find all the forces acting on the block and add them based on their direction to find the coefficient of friction. Here, the block is moving in a straight path, so, distance and displacement are the same and hence, speed and velocity will also be the same. The acceleration will be zero because velocity is constant, due to which the force acting on the body due to acceleration is zero. To solve this problem, we find the forces acting on the block and add them and equate them to zero.

Formula used:
Kinetic Friction force ${f_k} = \mu {F_N}$
Here, Kinetic Friction force is represented by ${f_k}$
Coefficient of kinetic friction is represented by $\mu$
Normal force is represented by ${F_N}$

Complete step by step solution:
Free body diagram of the block

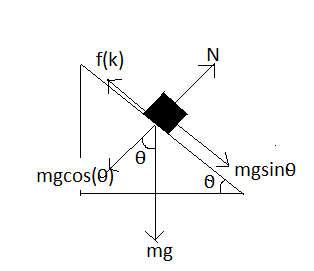
From the free body diagram, the normal force is equal to ${F_N} = mgcos\theta$
Friction force action between the block and the surface is equal to
${f_K} = \mu {F_N} = \mu mgcos\theta$
Adding all the forces along the plane of inclination
$mg\sin \theta - \mu mgcos\theta = ma$
Since the velocity is constant, acceleration is zero, and the force applied due to the acceleration is also zero.
Solving the equation, we get
$mg\sin \theta - \mu mgcos\theta = ma$
$mg\sin \theta - \mu mgcos\theta = 0$
$\Rightarrow \mu = \dfrac{{mg\sin \theta }}{{mgcos\theta }}$
$\Rightarrow \mu = \tan \theta$
Hence the coefficient of friction is equal to $\mu = \tan \theta$ for which the block moves at a constant speed.

Option (D) $\mu = \tan \theta$ is the correct answer.

Note: The angle of inclination at which the block just starts to move with a constant speed or acceleration along an inclined surface is called the Angle of Repose. It can also be defined as the maximum angle of inclination at which the block remains at rest. The angle of inclination is equal to the angle made by the weight of the body with its horizontal component.