Question
Question: A block \[A\] , whose weight is \(200\,N\) , is pulled up a slope of length \(5\,m\) by means of a c...
A block A , whose weight is 200N , is pulled up a slope of length 5m by means of a constant force F(=150N) as illuminated in figure. By how much has the potential energy of the block A increased?
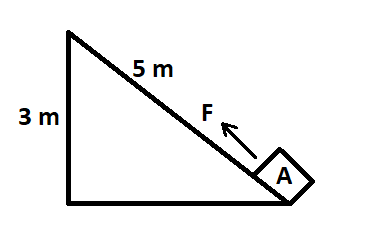
Solution
the potential energy is the energy that is stored by an object due to the new position relative to the position at zero. Here, in this above question, we first need to calculate the mass of the block. The increase in potential energy can be calculated by subtracting the potential energy at both positions.
Formula used:
Here, we will use Newton’s law of motion to calculate the mass of the block, which is shown below
F=ma
Here, F is the force, m is the mass of the force, and a is the acceleration due to gravity.
Here, we will take weight instead of force.
Also, the potential energy of the block is given by
P=mgh
Here, P is the potential energy, m is the mass of the block, and h is the height of the slope.
Complete step by step answer:
The above figure shows a slope of 5m on which a block A is placed. The weight of this block is 200N . This slope is pulled by a force of 150N as shown in the figure. Also, the height of the slope is 3m . Now, to calculate the mass of the block, we will use Newton’s second law of motion which is shown below
weight=mass×accelerationduetogravity
⇒200=m×10
⇒10200=m
⇒m=20kg
Now, to calculate the increase in potential energy of the block A , we will first calculate the potential energy at the ground and then we will calculate the potential energy at the top on the slope.
Now, the potential at the ground is given below
P1=m×g×h
⇒P1=20×10×0
⇒P1=0
Now, the potential at the top of slope is given by
P2=m×g×h
⇒P2=20×10×3
⇒P2=600Watt
Now the increase in the potential energy of the block A can be calculated by subtracting the potential at the ground from the potential at the top, which is shown below
P=P2−P1
⇒P=600−0
⇒P=600Watt
Hence, the increase in the potential energy of the block A is 600Watt .
Note:
Here, it is important to calculate the potential at the ground because we need to calculate the increase in potential energy. The increase in potential energy will occur due to the change in the positions of the block. Therefore, by subtracting the potential energy at both positions, we can calculate the potential energy.
