Question

A block $A$ of mass ${{m}_{1}}$ rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of the table and from its other end, another block B of mass ${{m}_{2}}$ is suspended. The coefficient of kinetic friction between the block and the table is $\mu_k$. When block A is sliding on the table, the tension in the string is:

Answer 1

Since the friction between block A and the table is not sufficient, the block B moves down due to its weight and pulls the block A which is connected by a string. If the block B moves down with acceleration $a$, then block A will also move horizontally with the same acceleration $a$.

Complete step by step solution:

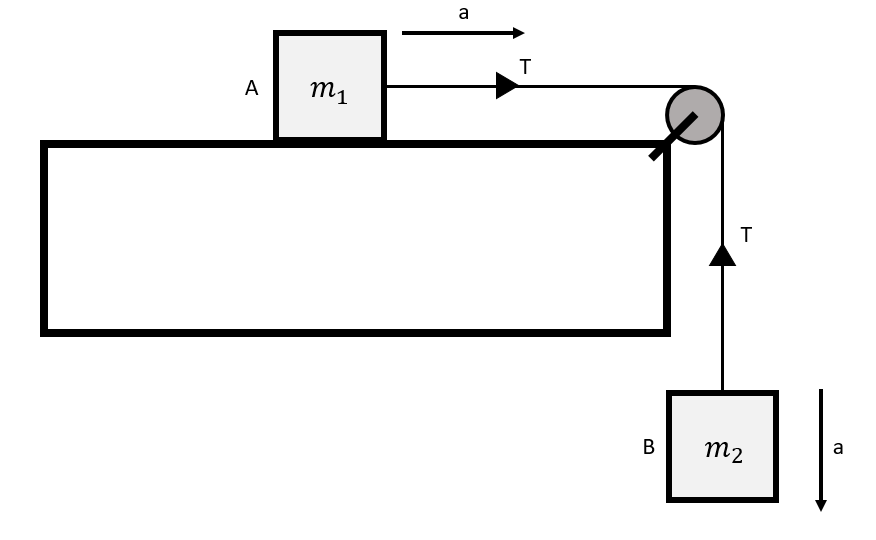
Here is the diagram of the block-pulley system as mentioned in the question. Now we will analyze the forces acting on each block from their free body diagram.
Free body diagram of block A

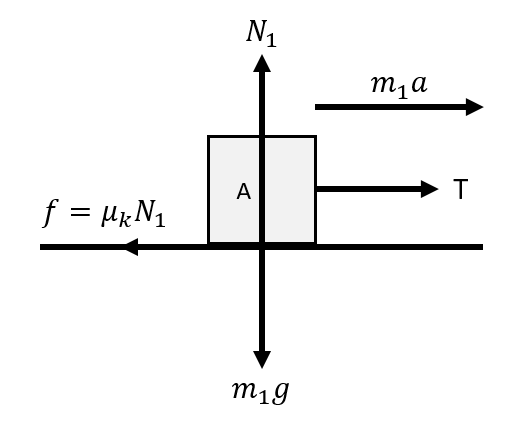
Here we see that the tension in the string pulls the block A of mass ${{m}_{1}}$ with an acceleration a. However, since the block is in contact with the table, it tries to pull the block backward due to kinetic frictional force $f$ between the block and the table. Therefore, if we balance the horizontal forces, we get

& T-f={{m}_{1}}a \\\ & T-{{\mu }_{k}}{{N}_{1}}={{m}_{1}}a \\\ \end{aligned}$$ $\Rightarrow T-{{\mu }_{k}}{{m}_{1}}g={{m}_{1}}a$ ………. (1) Here g is the acceleration due to gravity and ${{N}_{1}}$ is the normal reaction. Free body diagram for block B  Here we see that block B of mass ${{m}_{2}}$ is pulled down by its weight with acceleration $a$ and the tension T in the string tries to pull the block upwards. Therefore, if we balance the vertical forces, we get $\Rightarrow {{m}_{2}}g-T={{m}_{2}}a$ ………. (2) Now adding equations 1 and 2 and solving for $a$, we get $$\begin{aligned} & \Rightarrow {{m}_{2}}g-{{\mu }_{k}}{{m}_{1}}g={{m}_{1}}a+{{m}_{2}}a \\\ & \Rightarrow {{m}_{2}}g-{{\mu }_{k}}{{m}_{1}}g=({{m}_{1}}+{{m}_{2}})a \\\ & \Rightarrow a=\dfrac{({{m}_{2}}-{{\mu }_{k}}{{m}_{1}})g}{{{m}_{1}}+{{m}_{2}}} \\\ \end{aligned}$$ Substituting the value of $a$ in Eq. 2 and solving for T, we get $$\begin{aligned} & \Rightarrow {{m}_{2}}g-T={{m}_{2}}\dfrac{({{m}_{2}}-{{\mu }_{k}}{{m}_{1}})g}{{{m}_{1}}+{{m}_{2}}} \\\ & \Rightarrow T={{m}_{2}}g-{{m}_{2}}\dfrac{({{m}_{2}}-{{\mu }_{k}}{{m}_{1}})g}{{{m}_{1}}+{{m}_{2}}} \\\ \end{aligned}$$ On simplifying the above equation, we get $$\begin{aligned} & \Rightarrow T={{m}_{2}}g\left( 1-\dfrac{({{m}_{2}}-{{\mu }_{k}}{{m}_{1}})}{{{m}_{1}}+{{m}_{2}}} \right) \\\ & \Rightarrow T={{m}_{2}}g\left( \dfrac{{{m}_{1}}+{{m}_{2}}-{{m}_{2}}+{{\mu }_{k}}{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right) \\\ \end{aligned}$$ On further simplification, we get $$\begin{aligned} & \Rightarrow T={{m}_{2}}g\left( \dfrac{{{m}_{1}}+{{\mu }_{k}}{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right) \\\ & \Rightarrow T=\dfrac{{{m}_{1}}{{m}_{2}}(1+{{\mu }_{k}})g}{{{m}_{1}}+{{m}_{2}}} \\\ \end{aligned}$$ **$\therefore$ The tension in the string when the block A is sliding is $$T=\dfrac{{{m}_{1}}{{m}_{2}}(1+{{\mu }_{k}})g}{{{m}_{1}}+{{m}_{2}}}$$.** **Note:** Suppose in this case, if the friction between block A and the table would have been sufficient to prevent the sliding of block A. In that case, there would be no motion by either block (i.e. $a=0$), and in the equations, the coefficient of kinetic friction $\mu_k$ would be replaced by the coefficient of static friction $\mu_s$.