Solveeit Logo
Login

Question

Question: A block A of mass \(7\,Kg\) is placed on a frictionless table A thread tied to it passes over a fric...

A block A of mass 7 Kg7\,Kg is placed on a frictionless table A thread tied to it passes over a frictionless pulley and carries a body B of mass 3 Kg3\,Kg at the other end. The acceleration of the system is (given g=10 ms−2g = 10\,m{s^{ - 2}} )

A. 100 ms−2100\,m{s^{ - 2}}
B. 3 ms−23\,m{s^{ - 2}}
C. 10 ms−210\,m{s^{ - 2}}
D. 30 ms−230\,m{s^{ - 2}}

Explanation

Solution

In order to solve this question, first we will name the various force acting on both the blocks when system is released to move, and then by balancing all the forces acting on each block we will find the magnitude of acceleration of the system and remember since both blocks are attached to a string then both block A and B will have same acceleration which will be the acceleration of the system.

Complete step by step answer:
Let a be the acceleration of the system and T be the tension force acting on the sting and block B will start to move in downward direction whereas block A will start to move in forward direction and these various forces are shown as in the diagram. Since tension is the force acting on the string mBg,mBa{m_B}g,{m_B}a are the forces on block B whereas mAa{m_A}a is the force acting on block A.

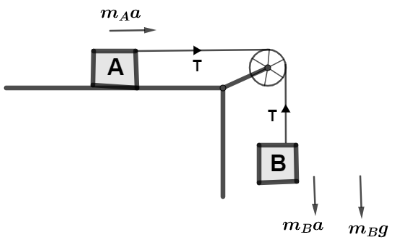
For block A the tension force is the only force which provide forward motion to block A so,
balancing both forces we have, T=mAa→(i)T = {m_A}a \to (i)Now, for block B , from diagram we can see that, weight and motion force mBg,mBa{m_B}g,{m_B}a are acting in downward direction balanced by tension T acting on string which can be written as
mBa=mBg−T→(ii){m_B}a = {m_B}g - T \to (ii)

From equation(i) put the value of T=mAaT = {m_A}a we get,
⇒(mB+mA)a=mBg\Rightarrow ({m_B} + {m_A})a = {m_B}g
now, as we have
mB=3Kg{m_B} = 3Kg
⇒mA=7Kg\Rightarrow {m_A} = 7Kg
⇒g=10 ms−2\Rightarrow g = 10\,m{s^{ - 2}}
putting the values in equation (mB+mA)a=mBg({m_B} + {m_A})a = {m_B}g we get,
(10)a=3(10)(10)a = 3(10)
∴a=3 ms−2\therefore a = 3\,m{s^{ - 2}}

Hence, the correct option is B.

Note: It should be remembered that, the surface between table and block A is frictionless and pulley is also frictionless that’s why there is no frictional force acting in whole system and force is a vector quantity so to solve such problems, always draw the various forces acting on the body with their directions and then solve for the required parameters.