Question

A block $A$ of mass $100Kg$ rests on another block $B$ of $200Kg$ and is tied to a wall as shown in the figure. The coefficient of friction between $A$ and $B$ is $0.2$ and that between $B$ and ground is $0.3$. The minimum force $F$ required to move the block $B$ is

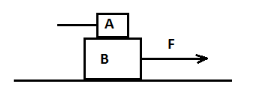
A.)$900N$
B.)$200N$
C.)$1100N$
D.)$700N$

Answer 1

Hint- For getting the unknown forces we should draw a free body diagram to resolve the forces and to get the clear idea of all the forces which are acting on each body separately. So here we will draw a diagram to resolve the forces.

Step By Step Answer:
Here in the diagram we see that there are so many forces like,
Friction force between block $A$and block $B$ = ${f_1}$
Friction force between block $B$ and the ground = ${f_2}$
Tension in the rope= $T$

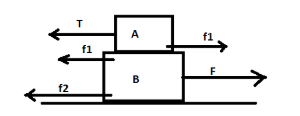
Minimum force required to move the block $B$=$F$

Given,

Mass of the block $A$=${m_A} =$ $100Kg$
Mass of block $B$=${m_B} =$ $200Kg$
Coefficient of friction between $A$and $B$=${\mu _1} =$ $0.2$
Coefficient of friction between $B$and ground=${\mu _2} =$ $0.3$

Frictional force acting between blocks A and B$= {f_1} = {\mu _1}{m_A}g = 0.2 \times 100 \times 10$

$\Rightarrow {f_1} = 200N$----equation (1)

Frictional force acting between block B and ground=$= {f_2} = {\mu _2}{m_B}g = 0.3 \times (100 + 200) \times 10$

$\Rightarrow {f_2} = 900N$------equation (2)

Now from the diagram we see that the minimum force that will be required to move the block $B$, will be such that it can overcome the friction forces( friction force between both blocks and the friction force between the ground and the block $A$). So, for minimum value it must be equal to the sum of both friction forces.

Hence the force required to move the block $A$
$F = {f_1} + {f_2}$ ------ equation (3)

Now putting the values from the equation (1) and equation (2) in the equation (3), we get
$F = 200 + 900 = 1100N$

Hence the required force will be $1100N$.

So, option (C) is the correct answer.

Note- Here the application of the friction force is there. Here we are experiencing two types of friction; one is static friction and another is kinetic friction. The friction which is keeping the block at rest is static friction, and after overcoming the static friction (when the block will start to move) the kinetic friction will come into action.