Question

A bird is sitting on a tree which is 80m high. The angle of elevation of a bird from a point on a ground is ${{45}^{\circ }}$ then the bird flies away from the point of observation horizontally and remains at a constant height. After 2 sec the angle of elevation from the point of observation becomes ${{30}^{\circ }}$. Find the speed of the flying bird.

Answer 1

The rough figure that represents the given information is shown below.

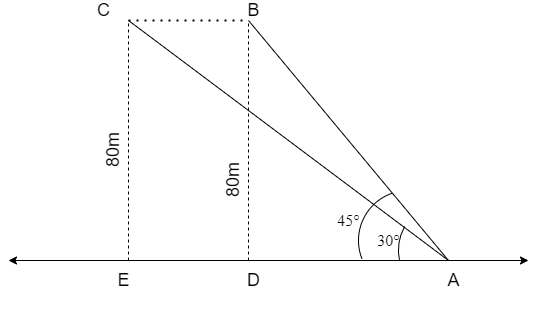
We solve this problem by using the simple formula of speed that is
$\text{Speed}=\dfrac{\text{Distance}}{\text{time}}$
For finding the distance we use the tangent trigonometric ratio formula that is
$\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$
By using this formula we calculate the distance travelled by bird in 2 sec to find the speed.

Complete step-by-step answer:
We are given that the bird is initially at a height of 80m at position B.
So, from the figure we can say that
$\Rightarrow BD=80m$
Let us assume that the bird moves to point C after 2 sec.
We are given that the bird maintains a constant height.
So, we can say that
$\Rightarrow CE=BD=80m$
We know that the tangent trigonometric ratio formula that is
$\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$
Now, let us consider the triangle $\Delta ABD$
Now, by applying the tangent trigonometric ratio formula we get
$\Rightarrow \tan {{45}^{\circ }}=\dfrac{DB}{DA}$
We know that from the standard table of trigonometric ratios we have
$\tan {{45}^{\circ }}=1$
Now, by substituting the required values in above equation we get

& \Rightarrow 1=\dfrac{80}{DA} \\\ & \Rightarrow DA=80 \\\ \end{aligned}$$ Now, let us consider the triangle $$\Delta ACE$$ Now, by applying the tangent trigonometric ratio formula we get $$\Rightarrow \tan {{30}^{\circ }}=\dfrac{CE}{EA}$$ We know that from the standard table of trigonometric ratios we have $$\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$$ Now, by substituting the required values in above equation we get $$\begin{aligned} & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{80}{EA} \\\ & \Rightarrow EA=80\sqrt{3} \\\ \end{aligned}$$ We know that from the figure the length ‘ED’ can be written as $$\Rightarrow ED=EA-DA$$ Now, by substituting the required values in above equation we get $$\begin{aligned} & \Rightarrow ED=80\sqrt{3}-80 \\\ & \Rightarrow ED=80\left( \sqrt{3}-1 \right) \\\ \end{aligned}$$ We are given that the bird maintain a constant height so, we can say that $$\Rightarrow BC=ED=80\left( \sqrt{3}-1 \right)$$ Let us assume that the speed of bird as $$'v'$$ We are given that the bird reaches point C after 2 sec so, we can take the time as $$\Rightarrow t=2$$ We know that the formula of speed that is $$\text{Speed}=\dfrac{\text{Distance}}{\text{time}}$$ By using the above formula we get the speed of bird as $$\Rightarrow v=\dfrac{BC}{t}$$ Now, by substituting the required values in above equation we get $$\begin{aligned} & \Rightarrow v=\dfrac{80\left( \sqrt{3}-1 \right)}{2} \\\ & \Rightarrow v=40\left( \sqrt{3}-1 \right) \\\ \end{aligned}$$ Therefore the speed of bird is $$40\left( \sqrt{3}-1 \right){}^{m}/{}_{s}$$ **Note:** Students may make mistakes for trigonometric ratio formula. We have the tangent trigonometric ratio formula that is $$\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$$ This formula is applicable only when the triangle is right angled triangle. But, students may use this formula for all types of triangles which is a blunder mistake. So, the formula significance needs to be taken care of.