Question

A bird is flying in a direction $30^\circ$ east of North with a speed of $5\;{\rm{km}}{{\rm{h}}^{ - 1}}$ and a cyclist is going on the road towards East at a speed of $10\;{\rm{km}}{{\rm{h}}^{ - 1}}$ The velocity of bird observed by cyclist is
A. $5\sqrt 3 \;{\rm{km}}{{\rm{h}}^{ - 1}}$ in a direction at $60^\circ$ West of North
B. $5\;{\rm{km}}{{\rm{h}}^{ - 1}}$ in North direction
C. $5\sqrt 3 \;{\rm{km}}{{\rm{h}}^{ - 1}}$ in a direction at $60^\circ$
D. $10\sqrt 3 \;{\rm{km}}{{\rm{h}}^{ - 1}}$ in a direction at $30^\circ$ West of North

Answer 1

First, we will draw the direction diagram for the velocity using the given statements. Then, the vectors will be written in terms of $x$ and $y$-components.

Complete step by step answer:
Given, the direction of flight of bird is $30^\circ$ east of North and the speed of the bird is $5\;{\rm{km}}{{\rm{h}}^{ - 1}}$ in that direction.

Now, the velocity diagram for the velocity of the bird and the velocity of the cyclist can be drawn as below.

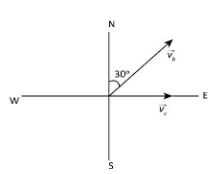
In the above diagram, the east west axis corresponds to the $X$ axis and the north-south axis corresponds to the $Y$ axis. So, we take the component of the velocity of the bird along the east west axis as $\left| {\overrightarrow {{v_b}} } \right|\sin \theta$ and the velocity along the north-south axis as $\left| {\overrightarrow {{v_b}} } \right|\cos \theta$ as shown in the vector diagram below.

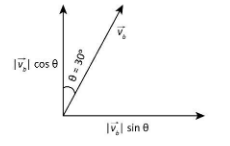
If we take $\theta = 30^\circ$ and ${\overrightarrow v _{_b}}$ as the velocity vector of the bird, then we can write
$\overrightarrow {{v_b}} = \left| {\overrightarrow {{v_b}} } \right|\sin \theta \widehat i + \left| {\overrightarrow {{v_b}} } \right|\cos \theta \widehat j$ ……(1)
The speed of the bird, $\left| {\overrightarrow {{v_b}} } \right| = 5\;{\rm{km}}{{\rm{h}}^{ - 1}}$. Hence, by substituting the values of $\left| {\overrightarrow {{v_b}} } \right|$ and $\theta$ in the equation (1), we get

$${\overrightarrow v _{_b}} = 5\sin 30^\circ \widehat i + 5\cos 30^\circ \widehat j\\\ \Rightarrow{\overrightarrow v _{_b}} = 5 \times \dfrac{1}{2}\widehat i + 5 \times \dfrac{{\sqrt 3 }}{2}\widehat j\\\ \Rightarrow{\overrightarrow v _{_b}} = \dfrac{5}{2}\widehat i + 5\dfrac{{\sqrt 3 }}{2}\widehat j$$

Let us take $\overrightarrow {{v_c}}$ as the velocity vector for the cyclist. Since the cyclist moves towards the east, we can define the velocity vector for him as,
$\overrightarrow {{v_c}} = \left| {\overrightarrow {{v_c}} } \right|\widehat i$
It is given that the cyclist moves in the east direction with speed $10\;{\rm{km}}{{\rm{h}}^{ - 1}}$. Therefore, $\left| {\overrightarrow {{v_c}} } \right| = 10\;{\rm{km}}{{\rm{h}}^{ - 1}}$. Since $\left| {\overrightarrow {{v_c}} } \right| = 10\;{\rm{km}}{{\rm{h}}^{ - 1}}$, we can write
$\overrightarrow {{v_c}} = 10\widehat i$
Hence, the velocity of the bird as observed by the cyclist can be written as
$\overrightarrow {{v_{bc}}} = \overrightarrow {{v_b}} - \overrightarrow {{v_c}} \\\ \Rightarrow\overrightarrow {{v_{bc}}} = \left( {\dfrac{5}{2}\widehat i + 5\dfrac{{\sqrt 3 }}{2}\widehat j} \right) - 10\widehat i\\\ \Rightarrow\overrightarrow {{v_{bc}}} = - \dfrac{{15}}{2}\widehat i + 5\dfrac{{\sqrt 3 }}{2}\widehat j$
Therefore, the magnitude of $\overrightarrow {{v_{bc}}}$ is
$\left| {\overrightarrow {{v_{bc}}} } \right| = \sqrt {{{\left( { - \dfrac{{15}}{2}} \right)}^2} + {{\left( {5\dfrac{{\sqrt 3 }}{2}} \right)}^2}} \\\ \Rightarrow \left| {\overrightarrow {{v_{bc}}} } \right| = \sqrt {\dfrac{{225}}{4} + \dfrac{{75}}{4}} \\\ \Rightarrow \left| {\overrightarrow {{v_{bc}}} } \right| = \sqrt {\dfrac{{300}}{4}} \\\ \Rightarrow \left| {\overrightarrow {{v_{bc}}} } \right| = \sqrt {75}$
Or
$\left| {\overrightarrow {{v_{bc}}} } \right| = 5\sqrt 3$
So, the velocity of the bird as observed by the cyclist is $5\sqrt 3 \;{\rm{km}}{{\rm{h}}^{ - 1}}$.

If we take $\overrightarrow {{v_{bc}}} = \left| {\overrightarrow {{v_{bc}}} } \right|\cos \phi \widehat i + \left| {\overrightarrow {{v_{bc}}} } \right|\sin \phi = - \dfrac{{15}}{2}\widehat i + 5\dfrac{{\sqrt 3 }}{2}\widehat j$, where $\phi$ is the angle made by the velocity vector $\overrightarrow {{v_{bc}}}$ with $\overrightarrow {{v_c}}$, then we can write
$\tan \phi = \dfrac{{\left| {\overrightarrow {{v_{bc}}} } \right|\cos \phi }}{{\left| {\overrightarrow {{v_{bc}}} } \right|\sin \phi }}$
It implies,
$\tan \phi = \dfrac{{\dfrac{{5\sqrt 3 }}{2}}}{{ - \dfrac{{15}}{2}}}\\\ \Rightarrow\tan \phi = - \dfrac{{\sqrt 3 }}{3}\\\ \Rightarrow\tan \phi = - \dfrac{1}{{\sqrt 3 }}$
We know,$\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$. Hence,
$\- \tan 30^\circ = - \dfrac{1}{{\sqrt 3 }}\\\ \Rightarrow\tan \left( {180^\circ - 30^\circ } \right) = \dfrac{{ - 1}}{{\sqrt 3 }}\\\ \Rightarrow\tan 150^\circ = \dfrac{{ - 1}}{{\sqrt 3 }}$
It implies, $\tan \phi = \tan 150^\circ$
Or
$\phi = 150^\circ \\\ \Rightarrow\phi = 90^\circ + 60^\circ$
From the above equation for angle, we can draw the velocity diagram for the velocity of the bird as observed by the cyclist as below.

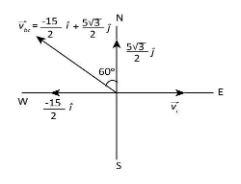
Therefore, the velocity of the bird as observed by the cyclist is $5\sqrt 3 \;{\rm{km}}{{\rm{h}}^{ - 1}}$ in a direction at $60^\circ$ west of north.

Hence, we can say that option A is correct.

Note: Please note that east of north and north of east implies different directions. If a person moves towards the east from the north axis, then the direction is referred to as east of north. If the person moves north from the east axis, then the direction is referred to as north of east. So,$30^\circ$ east of north means moving $30^\circ$ to the east from the north axis. Sometimes, we may confuse it as moving $30^\circ$ from the east to the north axis.