Question

A bird is flying $3\;m$ above the surface of water. If the bird is diving vertically down with speed of $6ms^{-1}$, its apparent velocity as seen by a stationary fish underwater is: ($\mu_{water} = \dfrac{4}{3}$):
A.$8\;ms^{-1}$
B.$6\;ms^{-1}$
C.$12\;^{-1}$
D.$4\;ms^{-1}$

Answer 1

Hint : We know that the distance and velocity can be deemed apparent over different media but time remains constant irrespective of the medium of propagation of light. Therefore, first find the time that the bird takes to reach the surface of the water. Then, using the fact that the refractive index of a medium gives the ratio of the apparent height to the real height, find the apparent height of the bird from the fish’s point of view. To this end, determine the apparent velocity from the apparent height and the constant time.

Formula Used:
Refractive index of a medium: $\mu = \dfrac{Apparent\;height}{Real\;height}$

Complete answer:
We have the light incident from the bird, going from the rarer medium to the denser medium, and the image of the bird as seen by the fish is projected from the denser to the rarer medium. In both cases there is bending of light rays due to the variational velocity of light travelling through the different media, owing to their different refractive indices. From the point of view of the fish, the bird appears to be further up than it actually is, say at B’ when it actually is at B.

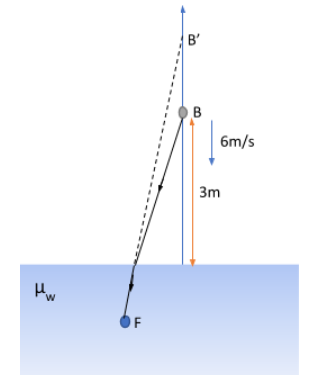
We are given that the initial actual height of the bird is $3\;m$. When viewed by the fish from the water, the bird appears to be further up than it actually is (at B’). This is because when light travels from the denser to a rarer medium the rays bend away from the normal, which projects the image beyond the height at which the object actually is.
Now in the case of the fish, as the bird swoops towards the water surface, it appears as though the bird is covering a larger distance in the given amount of time, which means that it appears to be diving in with a velocity greater than it actually is.
Now, the actual velocity of the bird is given as $v_{actual} = 6\;ms^{-1}$ and the actual distance it covers is $3\;m$.
Therefore, the time taken by the bird to reach the surface is given by: $t=\dfrac{3}{6} = 0.5\;m$
This is also the same amount of time that the bird takes from the perspective of the fish since time remains invariant over different media, but the height from which the bird flies and consequently the distance it covers will be apparent from the fish’s view.
We know that the refractive index of a medium: $\mu = \dfrac{Apparent\;height}{Real\;height}$
$\Rightarrow {h_{apparent}}=\mu_{water} \times h_{actual} = \dfrac{4}{3} \times 3 = 4\;m$
Thus, for the fish, the bird appears to be flying in from $4\;m$ away.
Therefore, the apparent velocity of the bird as seen by the fish will be:
$v_{apparent} = \dfrac{h_{apparent}}{t} = \dfrac{4}{0.5} = 8\;ms^{-1}$

Therefore, the correct option would be A. $8\;ms^{-1}$

Note:
Remember that when light travels from a rarer to a denser medium it bends away from the normal, whereas when light travels from a denser to a rarer medium it bends towards the normal. An optically denser medium impedes the speed of light whereas an optically rarer medium imparts a relatively higher speed to it. This is summarized by Snell’s Law:
$\dfrac{\mu_1}{\mu_2} = \dfrac{v_2}{v_1}$.