Question

A binary star consists of two stars A (mass 2.2 $M_s$) and B (mass 11 $M_s$), where $M_s$ is mass of the sun. They are separated by distance d and a rotation about their centre of mass, which is stationary. The ratio of the total angular momentum of the binary star to the angular momentum of start B about the centre of mass is
A. 6
B. 2
C. 3
D. 1

Answer 1

Determine the position of the two masses first then find the angular momentum based on the distances from the centre of mass. The centre of mass will become the axis and angular frequency about this will be the same for both the particles.
Formula used:
The angular momentum of a body about an axis is given by
$L = I \omega$
where I is the moment of inertia given by:
$I = mr^2$.

Complete answer:
Let the centre of mass be situated at the origin. Let $r_1$ be the distance of star A (to the left of origin) and $r_2$ be the distance of second star B from the centre of mass (origin).

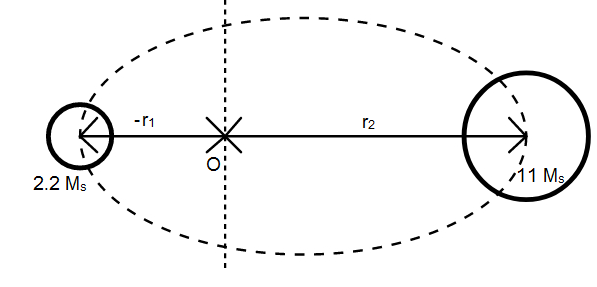
We are given
$r_2 - (-r_1) = d$
is the separation between the two bodies.
The position center of mass is given as:
$r_{CM} = \dfrac{m_1 r_1 + m_2 r_2}{m_1 + m_2 }$.
Making the substitutions according to our conditions, we may write:
$0 = \dfrac{2.2 M_s ( -r_1)+ 11 M_s (d - r_1 ) }{( 2.2 + 11) M_s}$
$\implies 11d = 13.2 r_1$ or,
$r_1 = \dfrac{5}{6} d$.
Now, $r_2 = \dfrac{1}{6} d$ becomes obvious.

The angular momentum of star B can be written as:
$L_B = I \omega = (11 M_s)\left( \dfrac{1}{6} d \right)^2 \omega$
The total angular momentum can be written as the sum of angular momentum of star A angular momentum of star B
$\implies L = (2.2 M_s)\left( \dfrac{5}{6} d \right)^2 \omega + (11 M_s)\left( \dfrac{1}{6} d \right)^2 \omega$
where we are substituted the respective distances from the centre of mass (or the axis) in the moment of inertia. A little simplification can give us:
$L = (2.2 \times 25 + 11) M_s \left( \dfrac{d}{6} \right)^2 \omega = 66 M_s \left( \dfrac{d}{6} \right)^2 \omega$ .
Taking the ratios now, we get:
$\dfrac{L}{L_B} = \dfrac{66 M_s \left( \dfrac{d}{6} \right)^2 \omega }{11 M_s \left( \dfrac{d}{6} \right)^2 \omega } = 6$.

So, the correct answer is “Option A”.

Note:
For the motion of two bodies around an axis, the total angular momentum can be written as a sum of angular momentum of the centre of mass and angular momentum for relative motion. This type of expression requires calculation of reduced mass for the system. The correct answer can be found using this too.