Question

A bimetallic strip is formed out of two identical strips, one of $Cu$ and the other of brass. The coefficients of linear expansion of the metals are ${{\alpha }_{c}}\text{ and }{{\alpha }_{b}}$. If on heating, the temperature of the strip goes up by $\Delta T$ and the strips bends to forms an arc of radius R, then R is, (This question has multiple correct answer)

$\begin{aligned} & \text{A}\text{. Proportional to }\Delta T \\\ & \text{B}\text{. Inversely Proportional to }\Delta T \\\ & \text{C}\text{. Proportional to }\left| {{\alpha }_{b}}-{{\alpha }_{c}} \right| \\\ & \text{D}\text{. Inversely proportional to }\left| {{\alpha }_{b}}-{{\alpha }_{c}} \right| \\\ \end{aligned}$

Answer 1

Hint: Since the bimetallic strips are identical, both the strips will have equal length and width. So in heating the bimetallic there will be a change in the length of the strip. If the strip bends and forms an arc of radius R, then the arc length is the final length after expansion.

Complete step by step answer:
Let $l\text{ and }w$ be the length and width of the two metallic strips before we start heating. Since the linear coefficient of copper and brass is different, the increase in length will be different for the copper strip and brass strip for the same range of temperature.

Let ${{l}_{c}}$ be the width of the copper strip after heating and ${{l}_{b}}$ be the length of the brass strip after heating. So we can write this increase as,

${{l}_{c}}=l\left( 1+{{\alpha }_{c}}\Delta T \right)$ ….. equation (1)
${{l}_{b}}=l\left( 1+{{\alpha }_{b}}\Delta T \right)$ ….. equation (2)

It is also given that the bimetallic strip on heating forms an arc of radius R. So let $\theta$ be the angle subtended by the arc at the center.

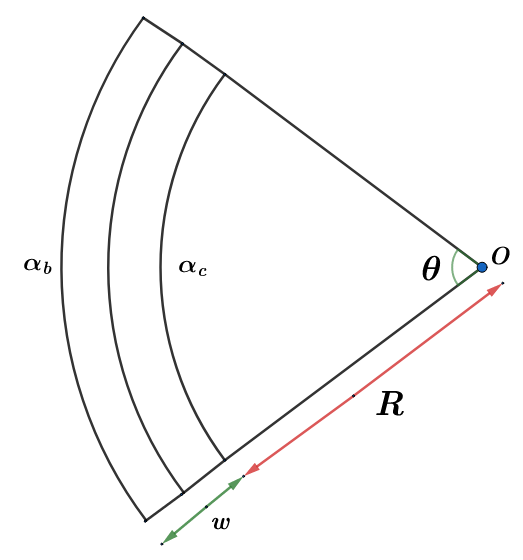
So the length of the copper strip after heating can be written as,

${{l}_{c}}=R\theta$ ….. equation (3)

The length of the brass strip after heating can be written as,

${{l}_{b}}=\left( R+w \right)\theta$ ….. equation (4)

Taking the ratio of equation (4) to equation (3), we get,

$\dfrac{{{l}_{b}}}{{{l}_{c}}}=\dfrac{R+w}{R}$
Substituting the values ${{l}_{b}}\text{ and }{{l}_{c}}$, from equation (1) and (2), we get

$\dfrac{l\left( 1+{{\alpha }_{b}}\Delta T \right)}{l\left( 1+{{\alpha }_{c}}\Delta T \right)}=\dfrac{R+w}{R}$
$\dfrac{\left( 1+{{\alpha }_{b}}\Delta T \right)}{\left( 1+{{\alpha }_{c}}\Delta T \right)}=1+\dfrac{w}{R}$
$\dfrac{w}{R}=\dfrac{\left( {{\alpha }_{b}}-{{\alpha }_{c}} \right)\Delta T}{1+{{\alpha }_{c}}\Delta T}$

Since $\alpha$ is very small, $1+{{\alpha }_{c}}\Delta T\approx 1$.

So, we can write,

$R=\dfrac{w}{\left| {{\alpha }_{b}}-{{\alpha }_{c}} \right|\Delta T}$

So R is inversely proportional to $\left| {{\alpha }_{b}}-{{\alpha }_{c}} \right|$ and $\Delta T$.
So the answer to the question is both option (B) and (D).

Note:
The coefficient of thermal expansion shows how the shape of an object changes with temperature. Which of the changes is evident depends on the object. For a long rod, whose surface area and volume is negligible, the thermal expansion of length is prominent. For a surface having surface area A, the thermal expansion is happening on the surface area. In other cases it is the volume that is being increased or decreased.

For an isotropic material, the expansion taking place is uniform in all the directions. Since it is uniform, we can express the coefficient of thermal expansion of area or volume in terms of linear coefficient of thermal expansion. We can write it as,

$\beta =2\alpha$

Where,

$\beta$ is the coefficient of thermal expansion in surface area.
$\alpha$ is the coefficient of thermal expansion in length.
$\gamma =3\alpha$
$\gamma$ is the coefficient of thermal expansion in volume.