Solveeit Logo
Login

Question

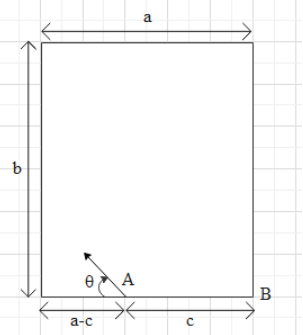
Question: A billiard table whose length and width are as shown in the figure. A ball is placed at point A. At ...

A billiard table whose length and width are as shown in the figure. A ball is placed at point A. At what angle θ\theta the ball be projected so that after colliding with two walls, the ball will fall in the pocket B. Assume that all collisions are perfectly elastic (neglect friction).

A. θ=cot⁡−1(2a−c2b)\text{A}\text{. }\theta ={{\cot }^{-1}}\left( \dfrac{2a-c}{2b} \right)
B. θ=tan⁡−1(2a−c2b)\text{B}\text{. }\theta ={{\tan }^{-1}}\left( \dfrac{2a-c}{2b} \right)
C. θ=cot⁡−1(c−a2b)\text{C}\text{. }\theta ={{\cot }^{-1}}\left( \dfrac{c-a}{2b} \right)
D. θ=cot⁡−1(c−ab)\text{D}\text{. }\theta ={{\cot }^{-1}}\left( \dfrac{c-a}{b} \right)

Explanation

Solution

When a particle collides elastically with a fixed surface making an angle θ\theta with the normal to the surface, the angle with the normal after collision is θ\theta . Use this theory to solve the given question.
tan⁡θ=opposite sideadjacent side\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}

Complete answer:
Let us first understand what happens when a particle hits a rigid surface and there is a perfectly elastic collision.
Suppose a ball hits a fixed surface with a velocity u making an angle θ\theta with the normal to the surface and a perfectly elastic collision takes place between the two. In this case, after the collision the ball will bounce back with the same velocity before the collision (i.e. u), making an angle θ\theta with the normal to the surface.
Now when apply the same concept to the given situation, we the path of the ball will be as shown below:

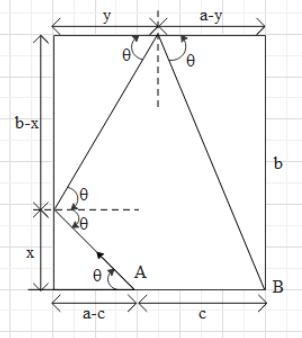
From ΔAGC\Delta AGC, we get that tan⁡θ=xa−c\tan \theta =\dfrac{x}{a-c}.
⇒x=(a−c)tan⁡θ\Rightarrow x=(a-c)\tan \theta ….. (i).
In ΔCED\Delta CED, we get that tan⁡θ=b−xy\tan \theta =\dfrac{b-x}{y} …. (ii).
Substitute the value of x from (i) in (ii).
⇒tan⁡θ=b−((a−c)tan⁡θ)y\Rightarrow \tan \theta =\dfrac{b-\left( (a-c)\tan \theta \right)}{y}
⇒y=b−((a−c)tan⁡θ)tan⁡θ\Rightarrow y=\dfrac{b-\left( (a-c)\tan \theta \right)}{\tan \theta }
⇒y=btan⁡θ−(a−c)tan⁡θtan⁡θ\Rightarrow y=\dfrac{b}{\tan \theta }-\dfrac{(a-c)\tan \theta }{\tan \theta }
⇒y=bcot⁡θ−(a−c)\Rightarrow y=b\cot \theta -(a-c) …. (iii).
In ΔDFB\Delta DFB, we get that tan⁡θ=ba−y\tan \theta =\dfrac{b}{a-y}
Substitute the value of y from (iii).
⇒tan⁡θ=ba−(bcot⁡θ−(a−c))\Rightarrow \tan \theta =\dfrac{b}{a-\left( b\cot \theta -(a-c) \right)}
⇒tan⁡θ=ba−(bcot⁡θ−a+c)\Rightarrow \tan \theta =\dfrac{b}{a-\left( b\cot \theta -a+c \right)}
⇒tan⁡θ=ba−bcot⁡θ+a−c\Rightarrow \tan \theta =\dfrac{b}{a-b\cot \theta +a-c}
⇒tan⁡θ=b2a−c−bcot⁡θ\Rightarrow \tan \theta =\dfrac{b}{2a-c-b\cot \theta }
⇒cot⁡θ=2a−c−bcot⁡θb\Rightarrow \cot \theta =\dfrac{2a-c-b\cot \theta }{b}
⇒cot⁡θ=2a−cb−bcot⁡θb\Rightarrow \cot \theta =\dfrac{2a-c}{b}-\dfrac{b\cot \theta }{b}
⇒cot⁡θ=2a−cb−cot⁡θ\Rightarrow \cot \theta =\dfrac{2a-c}{b}-\cot \theta
⇒2cot⁡θ=2a−cb\Rightarrow 2\cot \theta =\dfrac{2a-c}{b}
⇒cot⁡θ=2a−c2b\Rightarrow \cot \theta =\dfrac{2a-c}{2b}
⇒θ=cot⁡−1(2a−c2b)\Rightarrow \theta ={{\cot }^{-1}}\left( \dfrac{2a-c}{2b} \right)

Hence, the correct option is A.

Note:
One of the mistakes that a student may perform while solving this question is that he or she may pre assume that the first collision of the ball with the edge of table will be at the midpoint of the edge and the value of x will be equal to b/2.