Question

A billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at height h above its center, acquired a linear velocity${v_ \circ }$. The angular velocity${\omega _ \circ }$acquired by the ball is:
A. $\dfrac{{5{v_ \circ }{r^2}}}{{2h}}$
B. $\dfrac{{2{v_ \circ }{r^2}}}{{5h}}$
C. $\dfrac{{2{v_ \circ }h}}{{5{r^2}}}$
D. $\dfrac{{5{v_ \circ }h}}{{2{r^2}}}$
E. $\dfrac{{5{v_ \circ }{h^2}}}{{2{r^2}}}$

Answer 1

Hint: When a force acts on a body such that it gives it a rotational effect to the system then that acting force is known as torque. First, find torque that acts on the ball and equate it to height times the force that acts on it as well. Substitute the value of torque in terms of the moment of inertia and solve to obtain the required result.

Formula Used:
Torque,$\tau = I\alpha$
Moment of inertia of a spherical ball, $I = \dfrac{2}{5}m{r^2}$
Angular acceleration, $\alpha = \dfrac{{{\omega _ \circ }}}{t}$

Complete step-by-step answer:
Consider the following system of a spherical billiard ball of mass m and radius r, being hit by a force horizontal distance h above its center, as shown below:

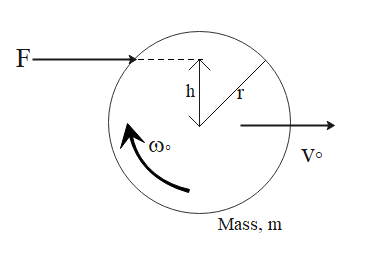
Clearly, the external force acting on the billiard ball results in Torque acting on the ball, this in turn makes the ball perform a rotating motion.
So the acting Torque on the ball can be given by:
\eqalign{ & \tau = I\alpha \cdots \cdots \cdots \left( 1 \right) \cr & {\text{where }}\tau {\text{ is the Torque,}} \cr & I{\text{ is the moment of inertia of the ball,}} \cr & \alpha {\text{ is the angular acceleration of the ball}}{\text{.}} \cr}
But the Torque acting on the ball must also be equal to the product of the external acting force, f and the perpendicular distance between the line of action of force from the axis of rotation.
$\Rightarrow \tau = F \times h \cdots \cdots \cdots \left( 2 \right)$
Equating equation (1) and (2), we get:
\eqalign{ & F \times h = I\alpha \cr & \Rightarrow Fh\sin {90^ \circ } = I\alpha \cr & \Rightarrow Fh = I\alpha \cr & \Rightarrow Fh = I\dfrac{{{\omega _ \circ }}}{t}{\text{ }}\left[ {\because \alpha = \dfrac{{{\omega _ \circ }}}{t}} \right] \cr}
But we know that the Moment of inertia of a spherical ball, $I = \dfrac{2}{5}m{r^2}$
$\Rightarrow Fh = \dfrac{2}{5}m{r^2}\dfrac{{{\omega _ \circ }}}{t}$
Also the applied force is equal to the product of mass and acceleration by Newton’s second law, so we get:
\eqalign{ & mah = \dfrac{2}{5}m{r^2}\dfrac{{{\omega _ \circ }}}{t} \cr & \Rightarrow m\dfrac{{{v_ \circ }}}{t}h = \dfrac{2}{5}m{r^2}\dfrac{{{\omega _ \circ }}}{t} \cr & \Rightarrow {v_ \circ }h = \dfrac{2}{5}{r^2}{\omega _ \circ } \cr & \therefore {\omega _ \circ } = \dfrac{{5{v_ \circ }h}}{{2{r^2}}} \cr}
Therefore, the correct option is D. i.e., $\dfrac{{5{v_ \circ }{h^2}}}{{2{r^2}}}$.

Note: The moment of inertia can be calculated for any object as the product of the mass of the object and its radius of gyration. The radius of gyration is nothing but a point having a radial distance in the system such that if the entire mass of the object is concentrated at that point it will have the exact same moment of inertia as the entire object.