Question

A big Diwali rocket is projected vertically upward so as to attain a maximum height of 160 m. The rocket explodes just as it reaches the top of its trajectory sending out luminous particles in all possible directions all with the same speed v. The display, consisting of the luminous particles, spreads out as an expanding, brilliant sphere. The bottom of this sphere just touches the ground when its radius is 80 m. With what speed (in m) are the luminous particles ejected by the explosion?

Answer 1

Note that all the particles travel with the same velocity $v$.All the particles after exploding moves in the shape of a brilliant sphere with expanding radius. This does not imply that the distance $d$ travelled by all the particles in the same time $t$ will be same, since for the particles moving in upward direction experience acceleration due to gravity in the opposite direction $( - g)$and the particle moving in the downward direction experience a positive acceleration $( + g)$.

Formula used: $s = ut + \dfrac{1}{2}a{t^2}$ , where $s$ is the displacement, $u$ is the initial velocity, $t$ is the time taken,$a$ is the acceleration.
$r = \dfrac{d}{2}$, $r$ is the radius, $d$ is the diameter.

Complete step by step answer:

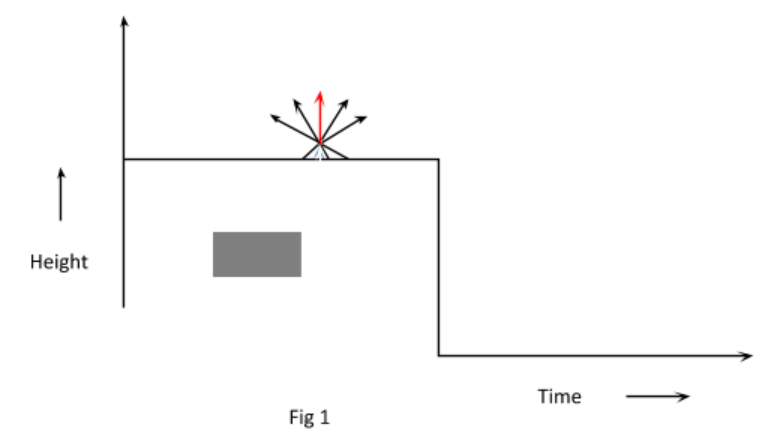
Initially the rocket reaches a maximum height of $160m$ and bursts into numerous luminous particles having the same velocity $v$. Let the explosion happen at time $t = 0$. Out of the numerous particles the one which travels straight upward and straight downward is shown by red and blue arrows respectively.

After time $t$

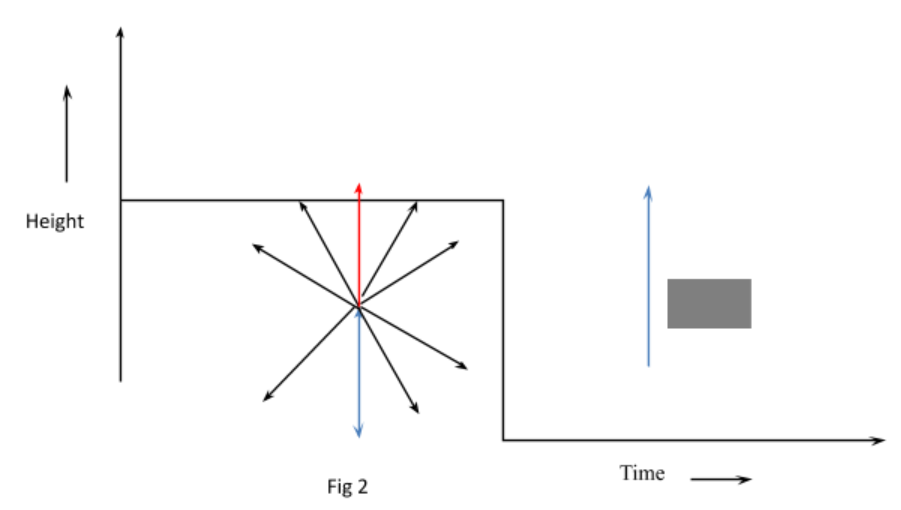
We can clearly see that the bottom point has reached the ground after $t$ seconds. Now the upward system is at a distance of $160m$ from the ground, Note that it is given in the question that it forms a sphere of radius $80cm$ when the bottom touches the ground. This implies that the top most point which is diametrically opposite will be at a distance $2 \times 80m$ =160m.

The bottom point travelled a distance of 160m with acceleration $g$ in time $t$.Using,$s = ut + \dfrac{1}{2}a{t^2}$

$160 = vt + \dfrac{1}{2}g{t^2}$=${d_1}$

The upper point travelled a distance ${d_2}$ in time $t$ with acceleration $- g$.Using,$s = ut + \dfrac{1}{2}a{t^2}$

${d_2} = vt - \dfrac{1}{2}g{t^2}$
Given $\dfrac{1}{2}({d_1} + {d_2}) = 80m$
We get $\dfrac{1}{2}(vt + \dfrac{1}{2}g{t^2} + vt - \dfrac{1}{2}g{t^2}) = 80m$
$vt = 80m$
Substituting this in equation $160 = vt + \dfrac{1}{2}g{t^2}$
$160 = 80 + \dfrac{1}{2}g{t^2}$
We get $t = 4s$
We know $vt = 80m$, therefore $v = 20m/s$

Note:
Using these values of $v$ and $t$, we can found out the value of ${d_2}$ which is the value of the total distance travelled by the top most point in 4 seconds .i.e. from the time of explosion to the time it reached 160m above ground (as shown in fig 2) We know ${d_2} = vt - \dfrac{1}{2}g{t^2}$. ${d_2} = 80 - \dfrac{1}{2} \times 10 \times 16 = 0$ we can say that he particle exploded from 160 m and in 4 s it reached back to the same position i.e. 160m above the ground .Therefore we got the displacement is zero.