Question
Question: A bicycle can go up a gentle inclination with constant speed where the frictional force of ground pu...
A bicycle can go up a gentle inclination with constant speed where the frictional force of ground pushing the rear wheel is F2=4N . With what force F1 must the chain pull on the socket wheel if R1=4cm and R2=30cm ?
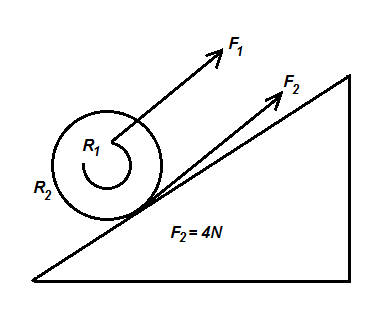
A. 4N
B. 24N
C. 140N
D. 435N
Solution
First of all, we will find the individual torques for the two different forces. After that we will equate both the equations as the net torque is zero for a body moving at constant speed. We will manipulate accordingly and obtain the result.
Complete step by step answer:
In the given problem, we are supplied with the following data:
The frictional force of ground pushing the rear wheel is the frictional force of ground pushing the rear wheel is 4N .
The radius of the rear socket wheel is 30cm .
The radius of the front socket wheel is 4cm .
We are asked to find the force F1 , with which the chain pulls on the socket wheel.
To begin with, we have to know that this problem is based on the rolling motion. Again, we can observe that the bicycle is moving up the inclined plane with a speed which is constant. This can be used to use the net force and the net torque is also zero.
First case:
The torque developed due to the force F1 can be expressed with the equation:
τ1=r1×F1 …… (1)
Where,
τ1 indicates the torque developed by the force.
r1 indicates the radius of the smaller socket wheel.
F1 indicates the force with which the chain pulls on the socket wheel.
Second case:
The torque developed due to the force F2 can be expressed with the equation:
τ2=r2×F2 …… (2)
Where,
τ2 indicates the torque developed by the force.
r2 indicates the radius of the smaller socket wheel.
F2 indicates the frictional force.
Since, the net torque is zero, we can write:
r1×F1=r2×F2F1=r1r2×F2 …… (3)
Substituting the required values in the equation (3), we get:
F1=530×4 F1=24NHence, the force with which the chain pulls on the socket wheel is 24N .
The correct option is B.
Note: It is important to note that if a rotatable object has a net torque of zero, it will be in rotational equilibrium and will not be able to obtain angular acceleration. Torque is therefore zero when the body is static.
