Question

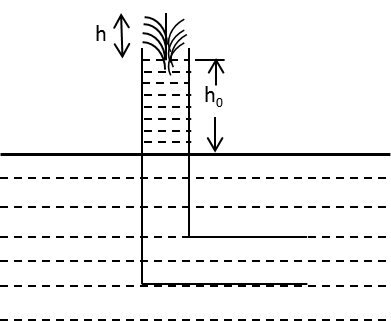
A bent tube is lowered into a water stream as shown in figure above. The velocity of the stream relative to the tube is equal to $V$. The closed upper end of the tube is located at the height ${h_0}$. The height $h$ to which the water jet spurted up is _ _ _.

A. $\dfrac{{{V^2}}}{{2g}} + {h_0}$
B. $\dfrac{{{V^2}}}{{2g}} - {h_0}$
C. $\dfrac{{2{V^2}}}{g} + {h_0}$
D. $\dfrac{{{V^2}}}{{2g}} + \dfrac{{{h_0}}}{2}$

Answer 1

Use Bernoulli's theorem which gives the relation between the velocities and heights of the water of water at both the ends of the tube. Use the concept of law of conservation of energy at the upper end of the tube.

Formula used:
The Bernoulli’s theorem is
${P_1} + \rho g{h_1} + \dfrac{1}{2}\rho v_1^2 = {P_2} + \rho g{h_2} + \dfrac{1}{2}\rho v_2^2$ …… (1)
Here, ${P_1}$ and ${P_2}$ are the pressures at the ends 1 and 2 of a pipe, $\rho$ is the density of the fluid, $g$ is the acceleration due to gravity, ${h_1}$ and ${h_2}$are the heights of the liquid at the ends 1 and 2 of the pipe and ${v_1}$ and ${v_2}$ are the velocities of the fluid at the ends 1 and 2 of the pipe respectively.
The kinetic energy $K$ of an object in terms of its density $\rho$ is
$K = \dfrac{1}{2}\rho v$ …… (2)
Here, $v$ is the velocity of the object.
The potential energy $U$ of an object in terms of its density $\rho$ is
$U = \rho gh$ …… (3)
Here, $g$ is the acceleration due to gravity.

Complete step by step answer:
A bent tube is lowered into a water stream as shown in figure above.
The velocity of the stream where it enters the tube is $V$. Let $V'$ be the velocity of the water when it comes out of the orifice.
The closed upper end of the tube is located at the height ${h_0}$.
The pressure $P$ of the water where it enters the tube and at the orifice are the same.
Apply Bernoulli’s theorem to the end of the tube where water enters in and the orifice from where water comes out.
$P + \rho g{h_1} + \dfrac{1}{2}\rho {V^2} = P + \rho g{h_0} + \dfrac{1}{2}\rho V{'^2}$
$\Rightarrow g{h_1} + \dfrac{1}{2}{V^2} = g{h_0} + \dfrac{1}{2}V{'^2}$
Here, ${h_1}$ is the height of the water where it enters the tube.
The height is zero for the present case.
Substitute $0\,{\text{m}}$ for ${h_1}$ in the above equation.
$g\left( {0\,{\text{m}}} \right) + \dfrac{1}{2}{V^2} = g{h_0} + \dfrac{1}{2}V{'^2}$
$\Rightarrow {V^2} = 2g{h_0} + V{'^2}$
Rearrange the above equation for $V{'^2}$.
$V{'^2} = {V^2} - 2g{h_0}$
According to the law of conservation of energy, when the water jumps out of the orifice, then all of its kinetic energy is converted into potential energy.
Hence, the kinetic energy of the water jumping out of the orifice is equal to the potential energy of the water at height $h$.
$\Rightarrow \dfrac{1}{2}\rho V{'^2} = \rho gh$
$\Rightarrow V{'^2} = 2gh$
Rearrange the above equation for $h$.
$h = \dfrac{{V{'^2}}}{{2g}}$
Substitute ${V^2} - 2g{h_0}$ for $V{'^2}$ in the above equation.
$h = \dfrac{{{V^2} - 2g{h_0}}}{{2g}}$
$\Rightarrow h = \dfrac{{{V^2}}}{{2g}} - {h_0}$
Therefore, the height to which the water spurts up is$\dfrac{{{V^2}}}{{2g}} - {h_0}$.

So, the correct answer is “Option B”.

Note:
The pressure at both the ends of the tube i.e. at the height h0 and where water enters the tube is equal to the atmospheric pressure.
It also follows the law of conservation of energy which states that when the water jumps out of the orifice, then all of its kinetic energy is converted into potential energy.