Solveeit Logo
Login

Question

Question: $|A|= \begin{bmatrix} 2k-1 & 2\sqrt{k} & 2\sqrt{k} \\ 2\sqrt{k} & 1 & -2k \\ -2\sqrt{k} & 2k & -1 \e...

∣A∣=[2k−12k2k2k1−2k−2k2k−1]|A|= \begin{bmatrix} 2k-1 & 2\sqrt{k} & 2\sqrt{k} \\ 2\sqrt{k} & 1 & -2k \\ -2\sqrt{k} & 2k & -1 \end{bmatrix}

Answer

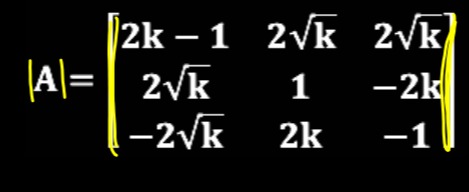
(2k+1)^3

Explanation

Solution

The determinant of the given 3x3 matrix was calculated using the cofactor expansion method. After expanding and simplifying the terms, the resulting polynomial in kk was recognized as the cubic expansion of (2k+1)3(2k+1)^3.

The determinant of a 3x3 matrix [abcdefghi]\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} is given by: ∣A∣=a(ei−fh)−b(di−fg)+c(dh−eg)|A| = a(ei - fh) - b(di - fg) + c(dh - eg)

Applying this to the given matrix: ∣A∣=(2k−1)∣1−2k2k−1∣−(2k)∣2k−2k−2k−1∣+(2k)∣2k1−2k2k∣|A| = (2k-1) \left| \begin{matrix} 1 & -2k \\ 2k & -1 \end{matrix} \right| - (2\sqrt{k}) \left| \begin{matrix} 2\sqrt{k} & -2k \\ -2\sqrt{k} & -1 \end{matrix} \right| + (2\sqrt{k}) \left| \begin{matrix} 2\sqrt{k} & 1 \\ -2\sqrt{k} & 2k \end{matrix} \right|

Calculating the 2x2 determinants:

  1. ∣1−2k2k−1∣=(1)(−1)−(−2k)(2k)=−1+4k2\left| \begin{matrix} 1 & -2k \\ 2k & -1 \end{matrix} \right| = (1)(-1) - (-2k)(2k) = -1 + 4k^2
  2. ∣2k−2k−2k−1∣=(2k)(−1)−(−2k)(−2k)=−2k−4kk\left| \begin{matrix} 2\sqrt{k} & -2k \\ -2\sqrt{k} & -1 \end{matrix} \right| = (2\sqrt{k})(-1) - (-2k)(-2\sqrt{k}) = -2\sqrt{k} - 4k\sqrt{k}
  3. ∣2k1−2k2k∣=(2k)(2k)−(1)(−2k)=4kk+2k\left| \begin{matrix} 2\sqrt{k} & 1 \\ -2\sqrt{k} & 2k \end{matrix} \right| = (2\sqrt{k})(2k) - (1)(-2\sqrt{k}) = 4k\sqrt{k} + 2\sqrt{k}

Substituting back: ∣A∣=(2k−1)(−1+4k2)−(2k)(−2k−4kk)+(2k)(4kk+2k)|A| = (2k-1)(-1 + 4k^2) - (2\sqrt{k})(-2\sqrt{k} - 4k\sqrt{k}) + (2\sqrt{k})(4k\sqrt{k} + 2\sqrt{k})

Expanding: Term 1: (2k−1)(4k2−1)=8k3−2k−4k2+1(2k-1)(4k^2-1) = 8k^3 - 2k - 4k^2 + 1 Term 2: −(2k)(−2k−4kk)=4k+8k2- (2\sqrt{k})(-2\sqrt{k} - 4k\sqrt{k}) = 4k + 8k^2 Term 3: (2k)(4kk+2k)=8k2+4k(2\sqrt{k})(4k\sqrt{k} + 2\sqrt{k}) = 8k^2 + 4k

Summing the terms: ∣A∣=(8k3−4k2−2k+1)+(4k+8k2)+(8k2+4k)|A| = (8k^3 - 4k^2 - 2k + 1) + (4k + 8k^2) + (8k^2 + 4k) ∣A∣=8k3+(−4k2+8k2+8k2)+(−2k+4k+4k)+1|A| = 8k^3 + (-4k^2 + 8k^2 + 8k^2) + (-2k + 4k + 4k) + 1 ∣A∣=8k3+12k2+6k+1|A| = 8k^3 + 12k^2 + 6k + 1

This is the expansion of (2k+1)3(2k+1)^3. (2k+1)3=(2k)3+3(2k)2(1)+3(2k)(1)2+13=8k3+12k2+6k+1(2k+1)^3 = (2k)^3 + 3(2k)^2(1) + 3(2k)(1)^2 + 1^3 = 8k^3 + 12k^2 + 6k + 1.