Solveeit Logo
Login

Question

Question: A beam of light wavelength \(600nm\) from a distance source falls on a single slit \(1mm\) wide, and...

A beam of light wavelength 600nm600nm from a distance source falls on a single slit 1mm1mm wide, and a resulting diffraction pattern is observed on a screen 2m2m away. The distance between the first dark fringes on either side of bright central fringe is
A. 1.2cm
B. 1.2mm
C. 2.4 cm
D. 2.4mm

Explanation

Solution

Hint: To solve this problem first we know about diffraction patterns. Diffraction of light is defined as the phenomenon of bending of light around the corners of an obstacle or an aperture into the region of geometrical shadow of the obstacle. This phenomenon is based on Huygens’s principle.
The diffraction of light is more pronounced when the dimensions of the obstacle are comparable with the wavelength of light. Size of obstacle depends upon the order of wavelength.

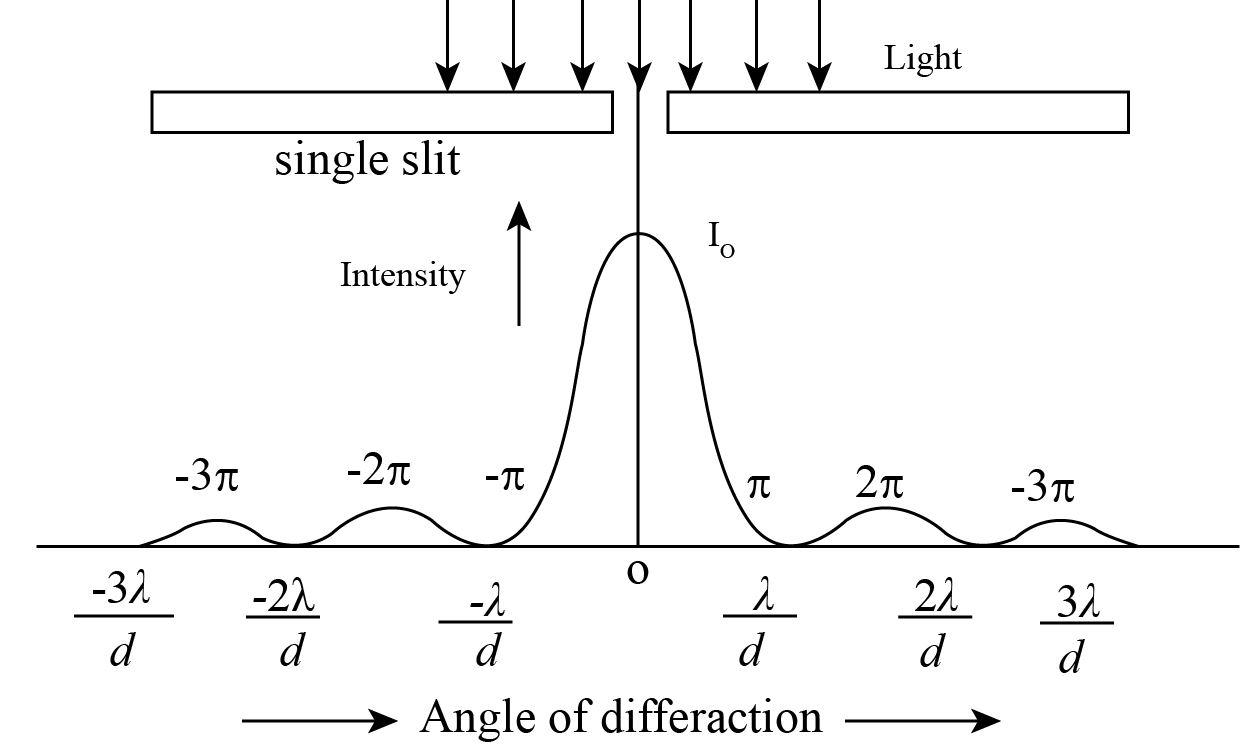
Complete step by step answer:
According to question single slit diffraction for the position of minima is dsin⁡θ=nλd\sin \theta = n\lambda
For a small value of θ\theta ,
sin⁡θ≈θ=yd\sin \theta \approx \theta = \dfrac{y}{d}
\eqalign{ & \therefore \dfrac{{dy}}{D} = \lambda \cr & \cr & \Rightarrow y = \dfrac{D}{d}\lambda \cr}
Now substitute all the values given in question;
λ\lambda =600nm=6×10−7m600nm = 6 \times {10^{ - 7}}m(wavelength)
D=2mD = 2m Distance, d=1mm=1×10−3md = 1mm = 1 \times {10^{ - 3}}m
\eqalign{ & y = \dfrac{{2 \times 6 \times {{10}^{ - 7}}}}{{1 \times {{10}^{ - 3}}}} \cr & \cr & = 1.2 \times {10^{ - 3}}m \cr & \cr & = 1.2mm \cr}

Therefore the distance between first dark fringe on either side of central maxima=2y2y =2.4mm = 2.4mm

Additional information: The essential condition for diffraction of light occurs is that wavelength of light should be comparable to that of the size of the object. Diffraction can also take place when the size of the object is less than the wavelength of the light.

Note: The diffraction grating is an important device that makes use of the diffraction of light to produce spectra. Diffraction is additionally fundamental in other applications like x-ray diffraction studies of crystals and holography. All waves are subject to diffraction once they encounter an obstacle in their path.