Question
Question: A beam of light on a glass hemisphere as shown. If the radius of curvature of the hemisphere is very...
A beam of light on a glass hemisphere as shown. If the radius of curvature of the hemisphere is very large in comparison to d, then the diameter of the beam at the base of the hemisphere will be:
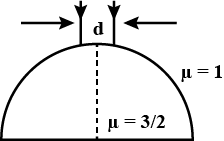
A. 43d
B. d
C. 3d
D. 32d
Solution
In order to solve this numerical let us draw a ray diagram according to the given data in the question, then by using the refraction formula we can calculate the diameter.
Complete step by step answer:
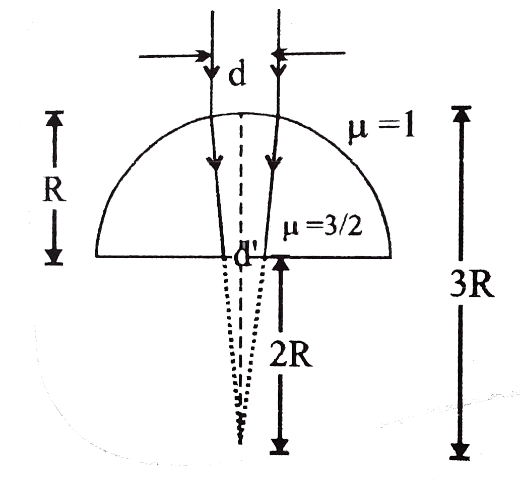
From the formula of refraction,
⇒vμ2−uμ1=Rμ2−μ1
⇒2v3−∞1=R3/2−1
⇒2v3=2R1
⇒v=3R
Hence the image distance is three times of R.
From the triangle,
Triangle ABE & triangle CDE are similar
3Rd=2Rd1
⇒d1=32d
Hence the correct option is D
Note: In the above question, If n = 1 then there is no refraction and the parallel rays should remain parallel, corresponding to x=∞.
For n = 1 the expression from a) yields the correct behavior.
