Question

A beam of light of wavelength 600 nm from a distant source falls on a single slit 1.0 mm wide and the resulting diffraction pattern is observed on a screen 2m away. What is the distance between the first dark fringes on either side of the central bright fringe?
A). $1.2cm$
B). $1.2mm$
C). $2.4cm$
D). $2.4mm$

Answer 1

Single slit formula gives the relation between the slit width, wavelength of the light beam, angle of refraction for different values of $n$. For smaller values of $n$, $\theta$ can be considered as zero. When $n=1$, the first dark fringe forms on either side of a central bright fringe. By substituting the values given, in the single slit formula, the distance can be found.
Formula used:
$d\sin \theta =n\lambda$

Complete step-by-step solution:

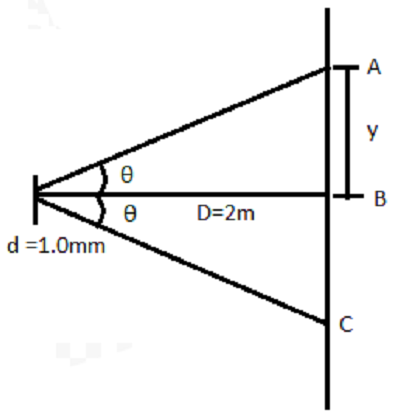
Let’s say, the first dark fringe formed at points A and C, and the central bright fringe at B. Here, the fringes formed on either side of the central fringe are symmetrical.
Hence, angle $\theta$ is the same for both fringes.
We have single slit diffraction formula,
$d\sin \theta =n\lambda$ --------- 1
Where,
$\theta$ is the angle from the center of the wall to the dark fringe
$n$ is a positive integer $\left( n=1,2,3..... \right)$
$\lambda$ is the wavelength of light
$d$ is the width of the slit
For small values of $\theta$, $\sin \theta \approx \theta$
The, from figure
$\theta =\dfrac{y}{D}$ ------- (2)
$\text{D}$ is the distance from slit to screen.
The distance between points A and B = The distance between B and C $\text{= y}$
Then, The distance between points A and C
$\text{= 2y}$
Substitute 2 in equation 1.
$d\dfrac{y}{D}=n\lambda$
Then,
$y=\dfrac{n\lambda D}{d}$
For$n=1$
$y=\dfrac{\lambda D}{d}$ --------- (3)
Given,
$\lambda =600\times {{10}^{-9}}m$,
$D=2m$, $d=1\times {{10}^{-3}}m$
Substitute the value of $\lambda$,$D$ and $d$ in equation 3
$y=\dfrac{600\times {{10}^{-9}}\times 2}{1\times {{10}^{-3}}}=1.2mm$
Therefore, $\text{Distance AC = 2y = 2}\times \text{1}\text{.2 = 2}\text{.4mm}$
Hence, the answer is option D.

Note: For the fixed values of $\lambda$ and $n$, as the $d$ gets smaller, $\theta$ increases and vice versa. From the single slit formula, we can understand that the wave effects are most noticeable when the wave encountering object (here, slits a distance $d$ apart) is small. Small values of $d$ give large values of $\theta$.