Question
Question: A beam of light is converging towards a point L. A plane parallel plate of glass of thickness t, ref...
A beam of light is converging towards a point L. A plane parallel plate of glass of thickness t, refractive index μ is introduced in the path of the beam. The convergent point is shifted by:
(Assume near normal incidence)
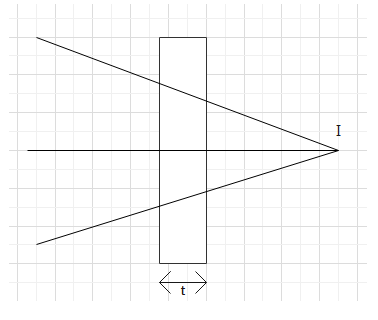
A. t(1−μ1)away B. t(1+μ1)away C. t(1−μ1)nearer D. t(1+μ1)nearer
Solution
Hint: When light passes from one medium to another it undergoes refraction. When it moves from rarer to denser medium, it shifts towards the normal and when it moves from denser to rarer medium; it bends away from the normal.
Formula used:
Snell’s Law: μ=sinrsini
where μ=refractive index, i=angle of incidence and r=angle of refraction.
∠I=∠e
where e is the angle of emergence.
For a very small value of θ, cosθ=1.
Complete step by step solution:
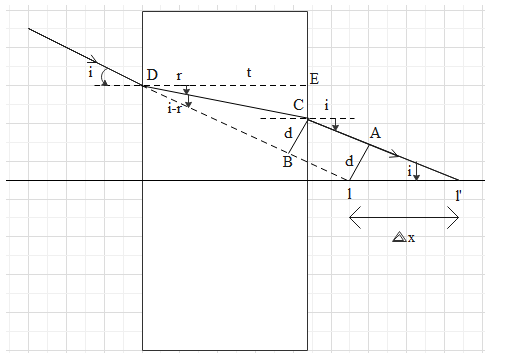
In this question, we have a glass plate of thickness t and refractive index μ. A light ray incident on the left side undergoes refraction, travels through the glass and then re-emerges on the right side as shown in the figure below.
If the ray had not undergone refraction then it would have gone straight but due to refraction, it bends and when it re-emerges, it is parallel and at distance of d from original ray. In order to calculate the distance Δx, we need to find this distance d first.
In right triangle DEC,
\cos r=\dfrac{DE}{DC}=\dfrac{t}{DC} \\\
\Rightarrow DC=\dfrac{t}{\cos r}\\\
In ΔCBD,
\sin (i-r) = \dfrac{BC}{DC} = \dfrac{d \cos r}{t} \\\
\Rightarrow d=\dfrac{t \sin (i-r)}{\cos r} \\\
\Rightarrow d=\dfrac{t (\sin i \cos r - \sin r \cos i)}{\cos r} \\\
\Rightarrow d= t \left(\sin i - \sin r \dfrac{\cos i}{\cos r} \right)\\\
In right ΔAl’l,
\sin i = \dfrac{Al}{ll’} = \dfrac{d}{\Delta x} \\\
\Rightarrow \Delta x = \dfrac{d}{\sin i} = t \left(\dfrac{\sin i}{\sin i} - \dfrac{\sin r}{\sin i} \dfrac{\cos i}{\cos r} \right) \\\
\Rightarrow \Delta x = t \left(1- \dfrac{1}{\mu} \dfrac{\cos i}{\cos r} \right)\\\
Here we have used Snell's law. The near normal incidence implies that the angle of incidence is very small, corresponding to which angle of refraction is also very small. Therefore, the final expression we have is
Δx=t(1−μ1)
And as we can see in the diagram, the ray is away from the direction of the original ray by a factor of Δx. Therefore, the correct answer is option A.
Note: Here, refractive index of glass is greater than air and image is formed farther but if it’s the opposite case then image will be formed nearer. It depends on the refractive index of a medium and greater the refractive index, more is the bending of light in that medium and vice-versa.
