Question

A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is (a) a convex lens of focal length 20 cm, and (b) a concave lens of focal length 16 cm?

Answer 1

Lens are the things, which will allow the light to pass through them with convergence or divergence. Depending on whether the lens will converge or diverge the rays they are divided into convex and concave lenses. Their capacity for convergence or divergence is given by the power of the lens. We have a lens equation to find out the position where the image is formed.
Formula used:
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$

Complete step-by-step solution
When an object is placed in front of the lens the rays from the object pass through the lens and suffer refraction and an image is formed. The position where the image forms and the nature of the image formed depends upon the type of lens we use.
Various positions of placing an object in front of a convex lens give us various positions of images.
If an object is placed between the pole and focus of the convex lens then the image will be formed on the same side of the lens. That image formed can be enlarged and virtual and erected.
Now if we place an object between focus and center then the image is formed away from the center and the image will be real and inverted. The size of the image will be bigger than an object.
For concave lenses, there is always a diminished virtual image formed on the same side of the lens.
Applying lens equation for convex lens
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Where ‘u’ is object distance and ‘v’ is the image distance and ‘f’ is focal length
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
\eqalign{ & \Rightarrow \dfrac{1}{v} - \dfrac{1}{{12}} = \dfrac{1}{{20}} \cr & \therefore v = 7.5cm \cr}
Ray diagram is given below

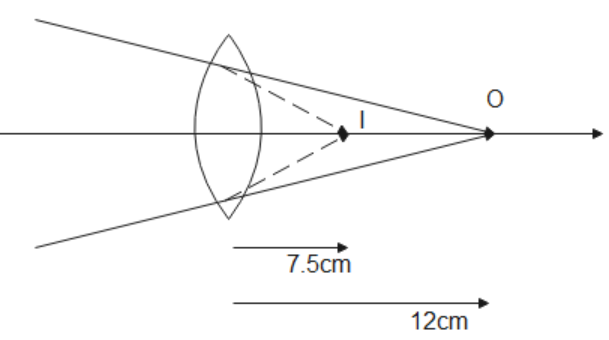
Applying lens equation for convex lens
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Where ‘u’ is object distance and ‘v’ is the image distance and ‘f’ is focal length
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
\eqalign{ & \Rightarrow \dfrac{1}{v} - \dfrac{1}{{12}} = \dfrac{1}{{ - 16}} \cr & \therefore v = 48cm \cr}
Ray diagram is given below

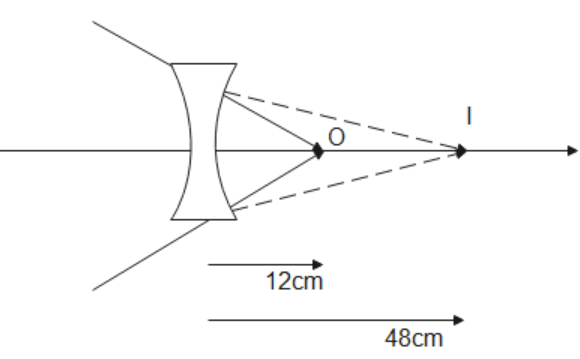
Note: Concave mirror can be analogous to convex lens. All the properties of the image formed by the concave mirror will be possessed by the image formed due to the convex lens. The only difference between the two images will be the side where images are formed. If images are formed on the object side in a concave mirror then images will be formed on the other side of the convex lens. Rest everything will be the same for the same position of objects in both cases. The same can be applied for convex mirrors and concave lenses.