Question
Question: A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards a...
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards as shown in the figure and whose equation is x2=ay. If the coefficient of friction is μ, the maximum height above the x-axis at which the particle will be in equilibrium is:
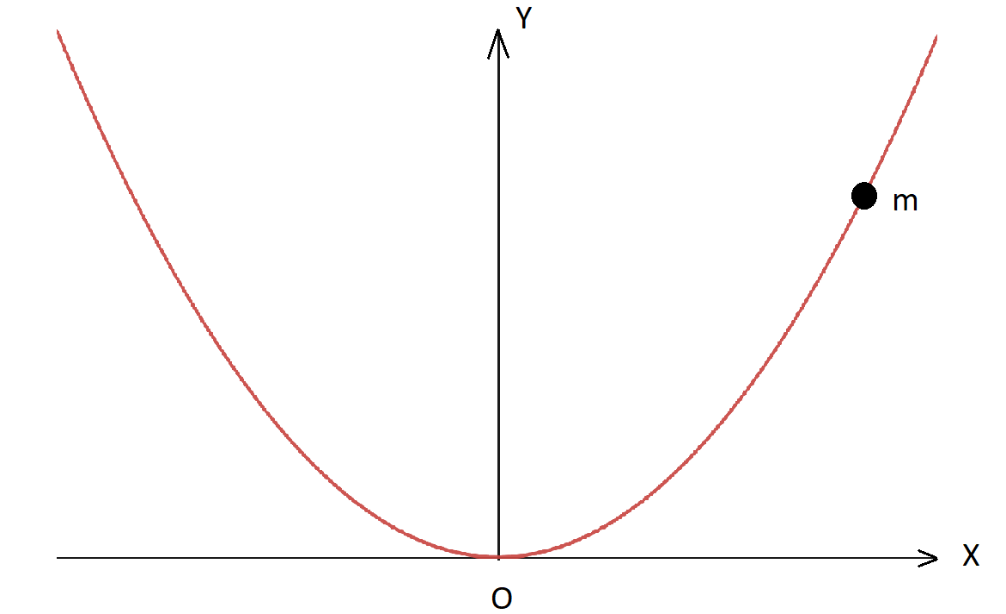
A) μa
B) μ2a
C) 4μ2a
D) 2μa
Solution
The coefficient of friction can be calculated and expressed in terms of the equation of motion. This can be done by drawing the free-body diagram of the bead and computing the forces acting on the bead when it is in motion along the curve.
Complete step by step answer:
Friction is a force that resists the relative motion between two solid surfaces, fluid layers, or material elements moving against one another. The frictional force acting on the body is dependent on the normal force acted upon by the surface on the body.
Frictional force,
F∝N
By removing the constant of proportionality, we have –
F=μN
where μ=coefficient of friction of the surface.
Consider a bead moving on the parabolic wire of equation x2=ay as shown.
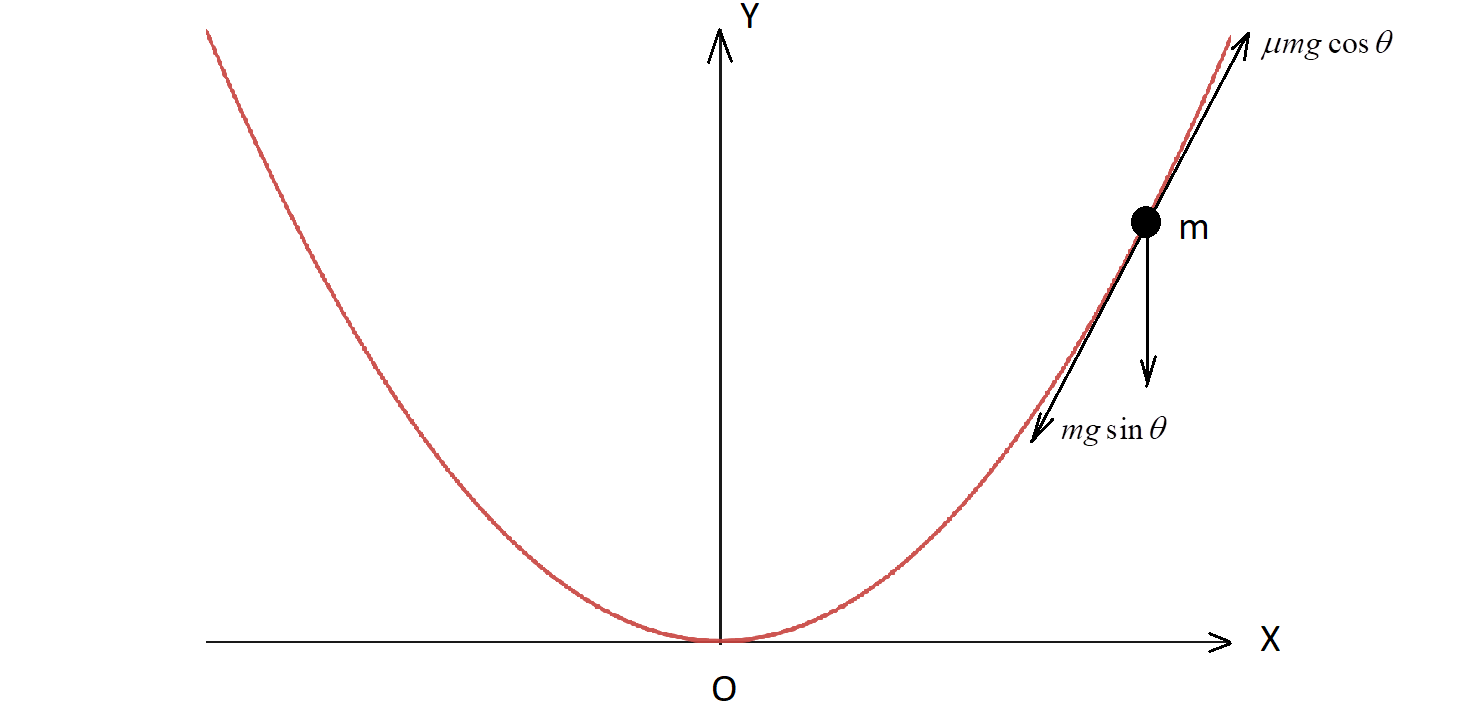
The forces act alongside the tangent drawn on the curve at the point where mass m is situated. The forces acting on the bead are:
i) Weight mg whose component mgsinθ acts along the tangent in the downward direction
ii) Frictional force acting in the opposite direction along the tangent, equal to μmgcosθ.
Since the bead is in equilibrium along the direction of the tangent, we have –
mgsinθ=μmgcosθ
⇒cosθsinθ=μ
⇒tanθ=μ
The slope of the tangent at any point is given by the tan of the angle made by the tangent with the horizontal.
However, the slope of the tangent is equal to the differential of the curve at the point. We have –
dxdy=tanθ
The equation of the parabola is –
x2=ay
⇒y=ax2
Differentiating the above equation, we get –
⇒dxdy=dxd(ax2)=a2x
Therefore, we have –
⇒a2x=tanθ
Substituting the result of tanθ from the derived equation, we have –
⇒a2x=μ
⇒x=2μa
The maximum distance above the x-axis travelled by the bead is equal to: x=2μa
Hence, the correct option is Option D.
Note: Students generally, confuse while writing the horizontal and vertical components of a vector. You can use a simple and handy thumb rule as shown here:
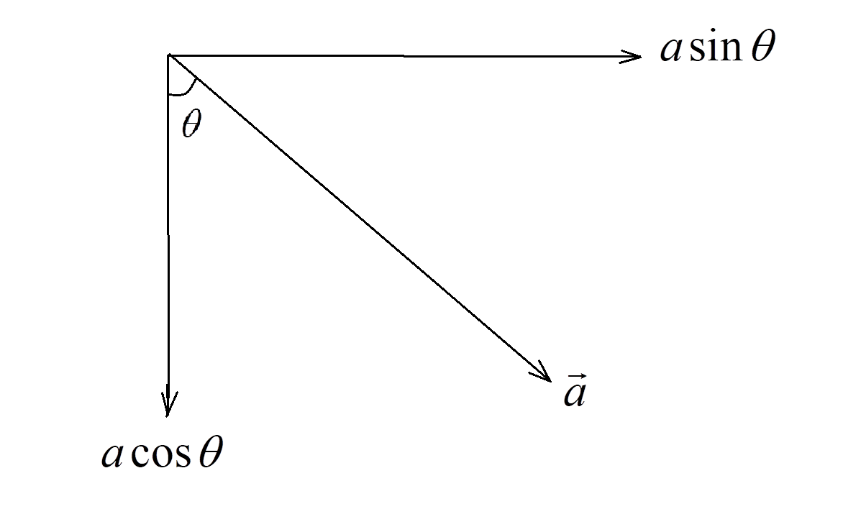
Consider a vector a inclined at angle θ as shown in the above figure:
- The line that is attached to the angle θ is designated as cosθ.
- The other line that is not attached to the angle θ is designated as sinθ.
