Question
Question: A bead of mass \[\dfrac{1}{2}\,{\text{kg}}\] starts from a rest A to move in a vertical plane along ...
A bead of mass 21kg starts from a rest A to move in a vertical plane along a smooth fixed quarter ring of radius 5m, under the action of constant horizontal force F=5N as shown. The speed of bead as it reaches the point B is: [Take g=10ms−2]
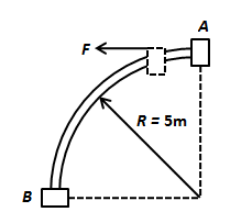
Solution
According to the work-energy theorem, the work done by the net force is equal to the change in kinetic energy. The work done by the bead is the sum of work done by the constant force and work done by the gravitational force. The initial kinetic energy of the bead is zero since it is started from the rest.
Formula used:
Work done by gravitational force, Wg=mgh
where, m is the mass, g is the acceleration due to gravity and h is the height from the ground.
Kinetic energy, K=21mv2
where v is the velocity.
Complete step by step answer:
We can observe that there are two forces acting on the bead: applied force of 5 N and the gravitational force which is pulling the bead downwards. We can calculate the work done by these two forces and then using the work energy theorem, we can calculate the velocity of the bead at position B.
The work done by the bead is the sum of work done by constant force and work done by gravitational force. Therefore,
W=WF+Wg
⇒W=Fscosθ+mgh
Here, F is the force, s is the displacement of the bead, θ is the angle between force F and displacement s, m is the mass of bead, g is the acceleration due to gravity and h is the change in height of the bead from its initial position.
Here, we can see, the constant force F and the displacement s are in the same direction and therefore, the angle between them is 0∘. Also, since the work done does not depend on the path, the displacement of the bead is the radius of the ring. Therefore,
W=Fscos(0)+mgh
⇒W=FR+mgR
Substituting F=5N, R=5m, m=21kg and g=10ms−2 in the above equation, we get,
W=(5)(5)+(21)(10)(5)
⇒W=25+25
⇒W=50J
Now, we have from the work-energy theorem, the work done by the net force is equal to the change in kinetic energy of the body. Here, the initial kinetic energy of the bead is zero since it is started from the rest.
W=21mv2
Here, v is the final velocity of the bead at position B.
Substituting W=50J and m=21kg in the above equation, we get,
50=21(21)v2
⇒200=v2
∴v=14.14m/s
Therefore, the velocity of the bead at position B is 14.14 m/s.
Note: We cannot say the decrease in the potential energy of the bead is equal to increase in the kinetic energy. This is true only when the body is allowed to move from the rest position. If the external force acts on the body along with the gravitational force, we have to calculate the work done by both the forces and then using the work-energy theorem, we can calculate the final kinetic energy.
