Question
Question: A battery of internal resistance \[4\,\Omega\] is connected to the network of resistance as shown. I...
A battery of internal resistance 4Ω is connected to the network of resistance as shown. In the order that the maximum power can be delivered to the network, the value of R in ohm should be
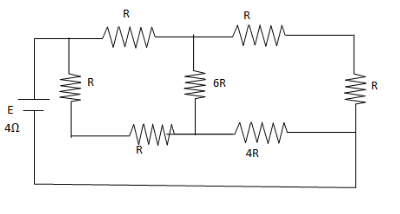
A. 94
B. 2
C. 38
D. 18
Solution
As, the given circuit is complicated so we first need to simplify the circuit. Then find the equivalent resistance of the circuit. We are asked to find the value of R when maximum power is delivered to the circuit. Recall the condition for which maximum power is delivered to the circuit.
Complete step by step answer:
Given, internal resistance of battery r=4Ω
We would need to find the equivalent resistance of the circuit, for that, first let’s name the branches.
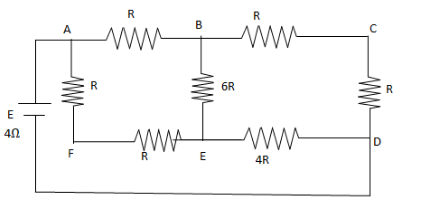
We observe that resistance of branch AF and FE are in series so equivalent resistance of branch AE will be,
