Question
Question: A battery of emf \({E_0} = 12V\)is connected across a 4m long uniform wire having resistance \(4\Ome...
A battery of emf E0=12Vis connected across a 4m long uniform wire having resistance 4Ωm−1. The cells of small emfs ε1=2Vand ε2=4Vhaving internal resistance 2Ω and 6Ω respectively, are connected as shown in the figure. If the galvanometer shows no deflection at point N, find the distance of point N from point A.
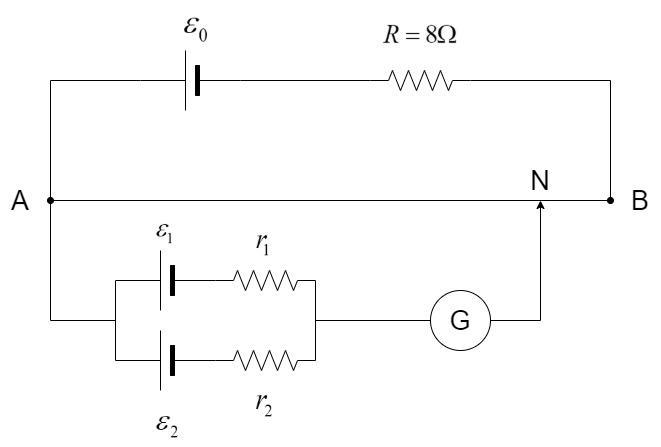
Solution
Hint : The circuit provided in the question is that of a device known as potentiometer. This problem can be solved by understanding the basic principle of potentiometer i.e. the voltage across the resistance is directly proportional to the length at which the galvanometer reads null deflection.
V∝l
V=kl
where k = voltage gradient of the potentiometer.
Complete step-by-step answer:
Potentiometer is a device used to calculate the emf and internal resistance of unknown cells by comparing them using a known value. It is loosely based on the principles of metre bridge, which is used to calculate the unknown resistances using the Wheatstone’s network.
It consists of a uniform wire AB, usually made of constantan. A steady current is maintained at one end of the wire AB and the other end is connected to the cells in study as shown in the circuit diagram below:
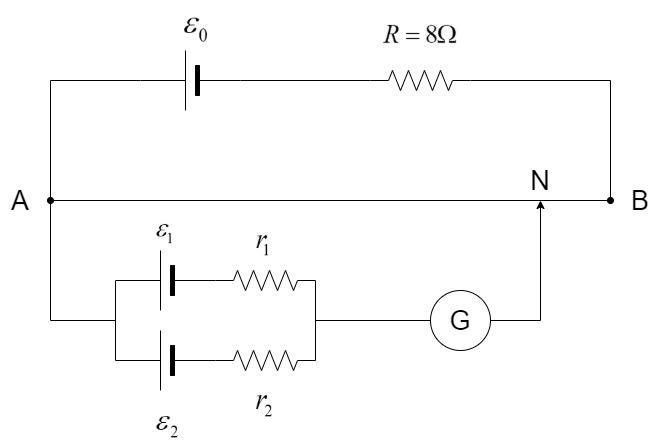
The potential gradient of the potentiometer is a constant value. It is taken as standard reference to calculate the emf and internal resistance on the other end of the circuit. The voltage on the other end of the circuit is given by –
V=KL
where K = potential gradient and L = length at which null point occurs.
To calculate potential gradient:
The potential gradient is calculated by finding the voltage across the wire AB and dividing it by the length of AB i.e. 4m.
The net resistance of AB, RAB = Length of AB × Resistance per unit length = 4×4=16Ω
Given, ε0=12V
Net resistance in the upper circuit, Rnet=R+RAB=8+16=24Ω
Current in the upper circuit, I=Rnetε0=2412=0⋅5A
Hence, voltage drop across AB, VAB=IRAB=0⋅5×16=8V
Given the length of AB, l=4m, the potential gradient of the wire,
K=lVAB=48=2Vm−1
To calculate net emf:
The net emf in the other end of the circuit is the combination of the emf and internal resistances of the two cells.
The equivalent emf is given by the formula –
V=r11+r21r1ε1−r2ε2
Given,
ε1=2V ε2=4V r1=2Ω r2=6Ω
Substituting, we get –
V=21+6122−64=6462=42=0⋅5V
Hence,
The net emf, V = 0.5V Potential gradient, K = 2 V/m
Therefore, length at null deflection is –
L=KV=20⋅5=0⋅25m
Thus, the length at which the galvanometer shows zero deflection is 0.25m.
Note: The reason for using constantan wire is, because the rate of change of resistivity per rise in temperature is very low. Hence, the resistance of the wire remains constant at a wide range of operating temperatures and gives accurate results.
